Aula

Lista de Exercícios

Aula 1-5: Movimento retilíneo uniformemente variado (MRUV)

Trata-se do movimento retílineo que é regido por uma velocidade que varia com taxa constante, ou seja, o movimento é sob linha e à velocidade variável; a variação ocorrerá mediante incrementos ou decrementos regulares no tempo de velocidade. A grandeza física que mede a alteração ade velocidade no tempo é a aceleração e, neste contexto, é constante.

Animação de veículo se deslocando em movimento retilíneo uniformemente variado, MRUV

Aceleração média

É a medida da taxa de variação da velocidade com respeito ao tempo. Podemos calculá-la extraindo-se a razão da variação de velocidade pelo intervalo de tempo correspondente a esta variação.

$a = \frac{\Delta v}{\Delta t}$

Movimento acelerado: Ocorre sempre que a aceleração e velocidade têm sentidos iguais (o corpo ganha velocidade sob efeito desta aceleração, ou seja, o módulo da velocidade aumenta).
Movimento retardado: Ocorre sempre que a aceleração e velocidade têm sentidos opostos (o corpo frena, perdendo velocidade sob efeito dessa aceleração; ou seja: o módulo da velocidade diminui).

Equação horária da velocidade

É uma equação capaz de nos fornecer a velocidade em função do tempo. Obtemos tal equação mediante manipulação algebrica da equação da aceleração.

$a = \frac{\Delta v}{\Delta t} = \frac{v -v_0}{t}\rightarrow v - v_0 = a.t$ $\rightarrow v = v_o + a.t\rightarrow$ $v = v_0 + a.t$

Equação horária do espaço

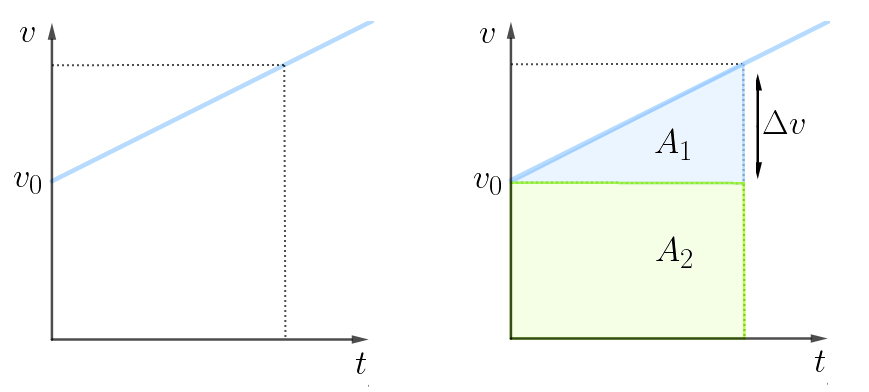
Sabemos que a área sobre um gráfico de velocidade em função do tempo fornece-nos o deslocamento do corpo estudado.

Gráficos usados para se deduzir a equação horária do espaço

$\Delta S = {\color{DarkGreen} A_1} + {\color{Blue} A_2} = {\color{DarkGreen} v_o.t} +{\color{Blue} \frac{1}{2}.\Delta v .t }.\frac{t}{t}$ $\rightarrow S - S_o = v_o . t + \frac{1}{2}.\frac{\Delta v}{t}. t^2$ $\rightarrow S = S_0 + v_o . t + \frac{a.t^2}{2}$

$S = S_0 + V_0.t + \frac{a.t^2}{2}$

Equação de Torricelli

É uma equação obtida a partir da manipulação algébrica das duas equações estudadas anteriormente. O resultado final é uma equação envolvendo três variáveis (deslocamento, velocidade e aceleração), como podemos perceber, essa equação não envolve o tempo, portanto, se se deseja resolver um problema em que o tempo não é dado nem pedido, provavelmente a equação de Torricelli poderá servir bem ao propósito.

Demonstração:

Primeiramente, isolaremos o tempo na equação horária da velocidade:

$v = v_o + a.t \rightarrow t = \frac{v - v_o}{a}$

Em seguinda, o substituíremos na equação horária do espaço:

$S = S_o +v_o.(v -vo) +\frac{a}{2}.(v - v_0)^2$

Após isso, basta manipularmos a expressão acima e, então, obteremos a fórmula final:

$v^2 = v_0^2 + 2 . a . \Delta S$

Gráficos do MRUV

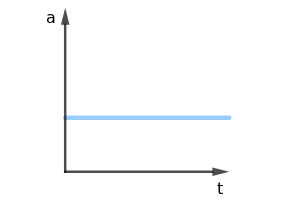
ACELERAÇÃO X TEMPO

Por estarmos lidando com uma variação uniforme de movimento, teremos uma aceleração (taxa de variação de velocidade) constante (pois é uniforme) diferente de 0. O gráfico será, então, sempre uma reta horizontal.

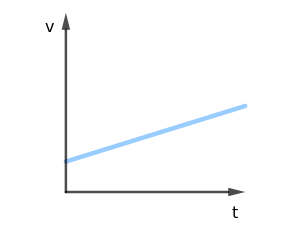
VELOCIDADE X TEMPO

O gráfico da velocidade apresentará uma reta oblíqua crescente quando a aceleração for positiva e, quando for negativa, uma reta decrescente. O ponto em que esta reta cruza o eixo vertical demarca a velocidade inicial do móvel.

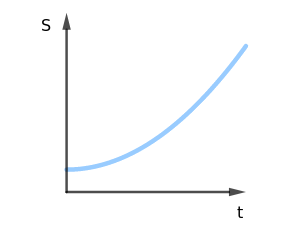
ESPAÇO X TEMPO

O gráfico do espaço em função do tempo sempre nos apresenterá uma parábola. A concavidade da parábola estará voltada para cima quando a aceleração for positiva e, para baixo, quando for negativa. O ponto em que o gráfico cruza o eixo vertical demarcará a posição inicial do móvel.

Gráfico característico da aceleração pelo tempo em MRUV

Gráfico característico da velocidade pelo tempo em MRUV

Gráfico característico do espaço pelo tempo em MRUV