Aula
Aula 
Aula 1-10: Movimento harmônico simples (MHS)

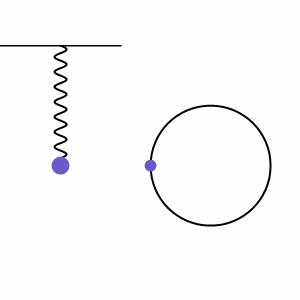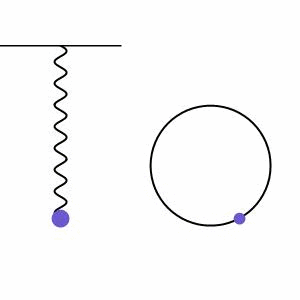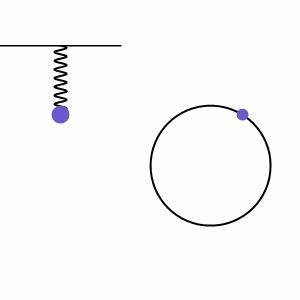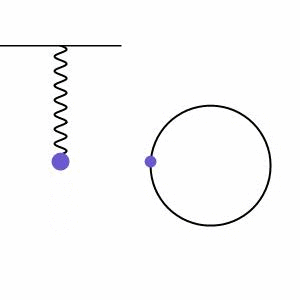
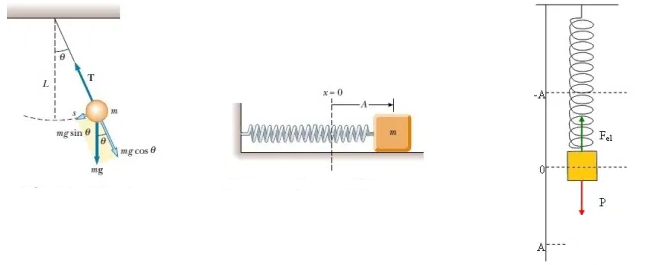
Chamamos de movimento harmônico simples (MHS) o movimento oscilatório que se dá ao redor de uma posição de equilíbrio. As oscilações deste tipo de movimento se repetem periodicamente, isto é, em intervalos de tempo iguais. São exemplos de MHS pêndulos em oscilações de amplitude pequena e sistemas massa-mola, quando desprezamos as resistências envolvidas nos sistemas.
|
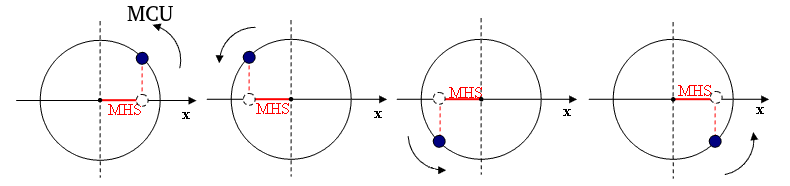
É matematicamente verídico que todo movimento harmônico simples é a projeção em um eixo de um movimento circular uniforme:
Uma vez percebido isto, interessa-nos, aqui em cinemática, descrevermos o espaço, velocidade e aceleração do MHS a partir de funções. |
|
Função da posição
|
|
Uma breve análise algébrica do triângulo destacado ao lado, permite-nos inferir que a posição da partícula dar-se-á por: Em que A, que é igual ao raio R, é a amplitude, isto é, a maior distância possível que haverá entre a artícula e o ponto de equilíbrio. Dos estudos de movimento circular, sabemos que o ângulo Substituindo esta expressão na equação anteriormente encontrada, teremos: |
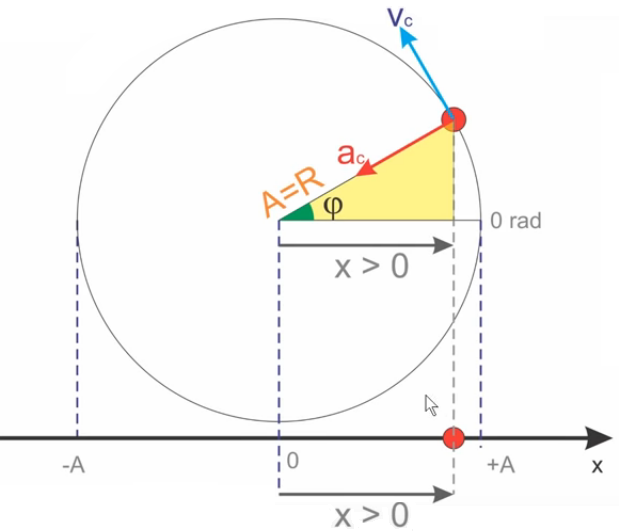
Uma breve análise algébrica do triângulo destacado ao lado, permite-nos inferir que a posição da partícula dar-se-á por:
Em que A, que é igual ao raio R, é a amplitude, isto é, a maior distância possível que haverá entre a artícula e o ponto de equilíbrio.
Dos estudos de movimento circular, sabemos que o ângulo é dado pela expressão:
Substituindo esta expressão na equação anteriormente encontrada, teremos:
Função da velocidade
|
|
O triângulo destacado nos permite inferir que: Em que Dos estudos de movimento circular, sabemos que o a velocidade tangencial pode ser escrita em função da velocidade angular e do raio: Substituindo este valor na equação anteriormente encontrada, teremos: |
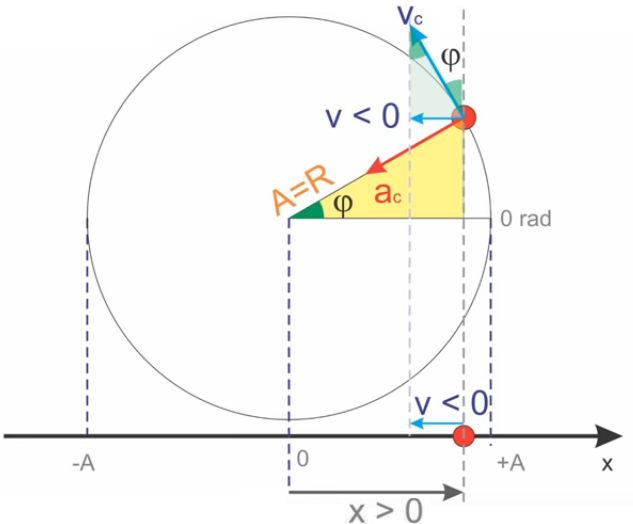
O triângulo destacado nos permite inferir que:
Em que é a velocidade tangencial do movimento circular uniforme.
Dos estudos de movimento circular, sabemos que o a velocidade tangencial pode ser escrita em função da velocidade angular e do raio:
Substituindo este valor na equação anteriormente encontrada, teremos:
Função da aceleração
|
|
O triângulo destacado nos permite inferir que: Em que Dos estudos de movimento circular, sabemos que o a velocidade tangencial pode ser escrita em função da velocidade angular e do raio: Substituindo este valor na equação anteriormente encontrada, teremos: |
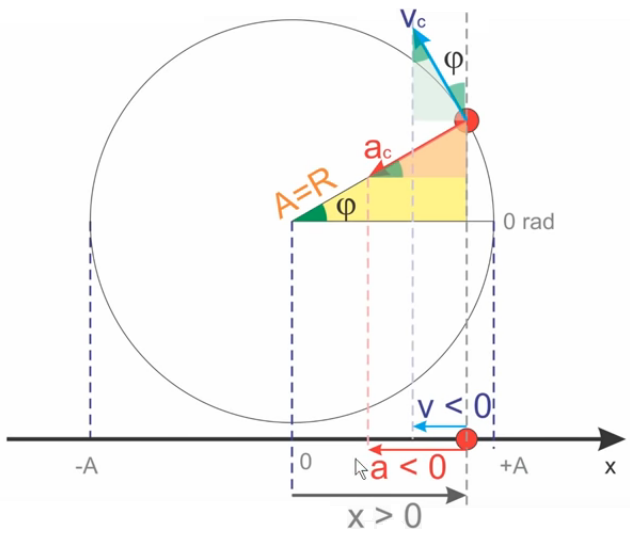
Em que é a aceleração tangencial do movimento circular uniforme.
Dos estudos de movimento circular, sabemos que o a velocidade tangencial pode ser escrita em função da velocidade angular e do raio:
Substituindo este valor na equação anteriormente encontrada, teremos:
Gráficos da posição, velocidade e aceleração em função do tempo
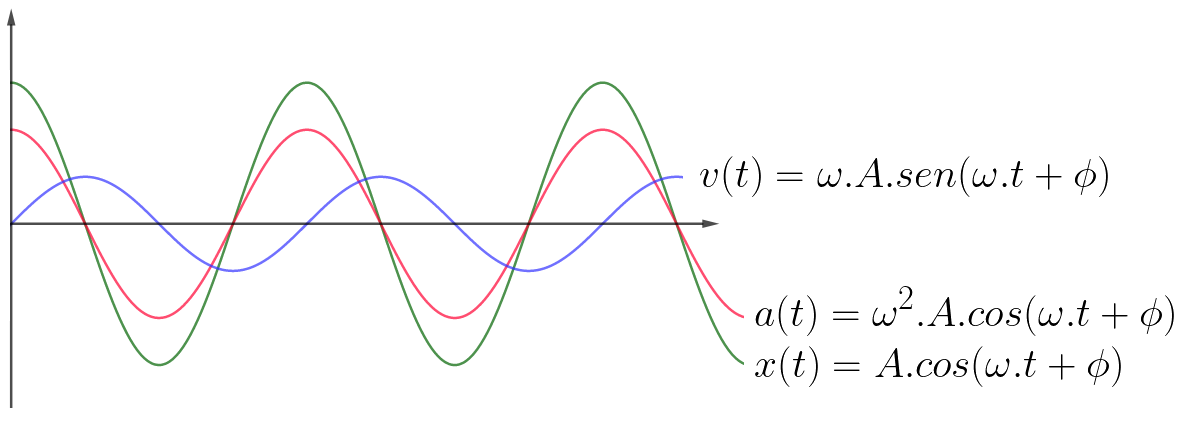
A força restauradora
De acordo com o que há pouco deduzimos:
e
; ou seja:
Sabemos, por meio da segunda lei de Newton que , substituindo este valor na equação encontrada anteriormente, teremos:
, em que
é constante.
Daí concluímos que os movimentos ditos oscilatórios são aqueles cujas forças restauradoras são do tipo: