Aula
Aula 
Aula 12-93: Transformadas de Lorentz

Transformadas de Lorentz (Abordagem de Lorentz)
|
Tão logo que surgiu as equações de maxwell, os cientistas perceberam que a aplicação das transformadas de Galileu para descrever o compotamento de ondas eletromagnéticas em outros referenciais apresentava graves problemas do ponto de vista físico. Na intenção de romper com as contradições da física de seu tempo, Um cientista holândes, Hendrik Lorentz (★ 1853 — 1928 ✝), tentou curar as transformadas de Galileu sugerindo haver um fator de correção |
|
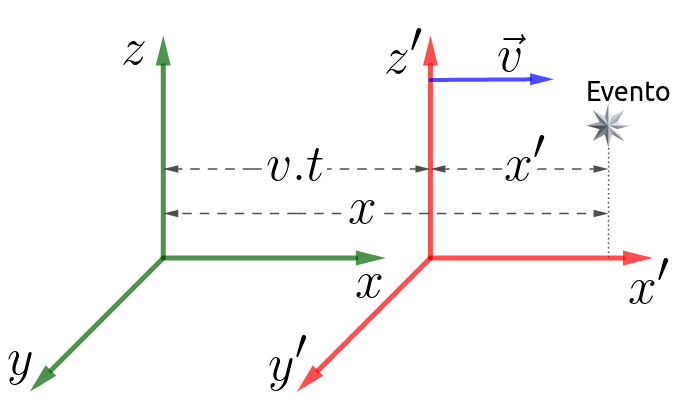
➔ TRANSFORMADAS DE GALILEU
|
|
|
|
➔ TENTATIVA DE CORREÇÃO
|
Observe que agora diferenciaremos as notações para os tempos marcados em diferentes referenciais, pois nada nos garante que os tempos passem igualmente em ambos.
|
|
|
Substituindo x' na quação de x, teremos:
Note que t e t', sengundo a correção proposta, agora já não mais se equivalem, e que dependem do espaço.
Reesecrevendo o que obtivemos até aqui:
|
|
|
|
Para encontrarmos o valor do fator de correção, admitiremos como premissa que a velocidade da luz é contante igual a c. Ou seja, a velocidade da luz é a mesma para os dois referenciais.
Imaginemos agora que um feixe de luz foi disparado em um dos referenciais, em t = 0, então:
Observe que o termo entre colchetes deve valer 1:
Em posse agora do valor de correção, temos as transformadas de Lorentz:
TRANSFORMAÇÃO de S em S' |
TRANSFORMAÇÃO de S' em S |
Transformadas de Lorentz (Abordagem de Einstein)
Os postulados da relatividade são:
1. As leis da física são as mesmas para quaisquer referenciais; não existe referencial privilegiado.
2. A velocidade da luz no vácuo tem o mesmo valor para todos os referenciais.
|
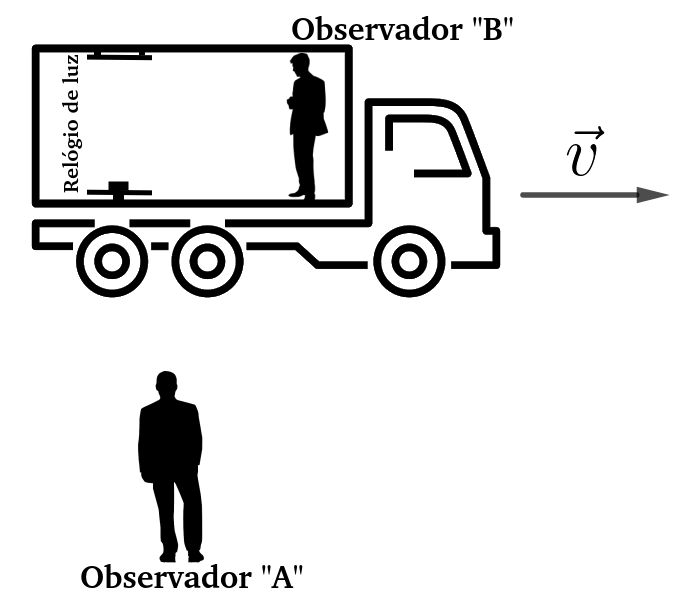
Imagine a seguinte situação: Dentro de um automóvel existe um relógio de luz, o seu funcionamento consiste em disparar do chão do veículo um pulso de luz que, ao ser disparado em direção ao teto, encontra lá um espelho que o reflete, fazendo-o retornar ao ponto de disparo onde ele é capturado novamente. O tempo marcado por este relógio corresponde ao tempo necerrário para que este processo seja executado. Dentro do veículo temos um observador, que chamaremos de B. Junto a superficie terrestre, observando o automóvel que se move, temos o observador A. |
|
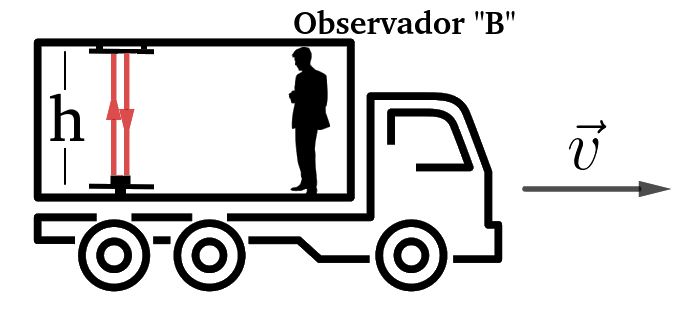
TEMPO DECORRIDO PARA O EVENTO SEGUNDO O OBSERVADOR "B"
|
|
|
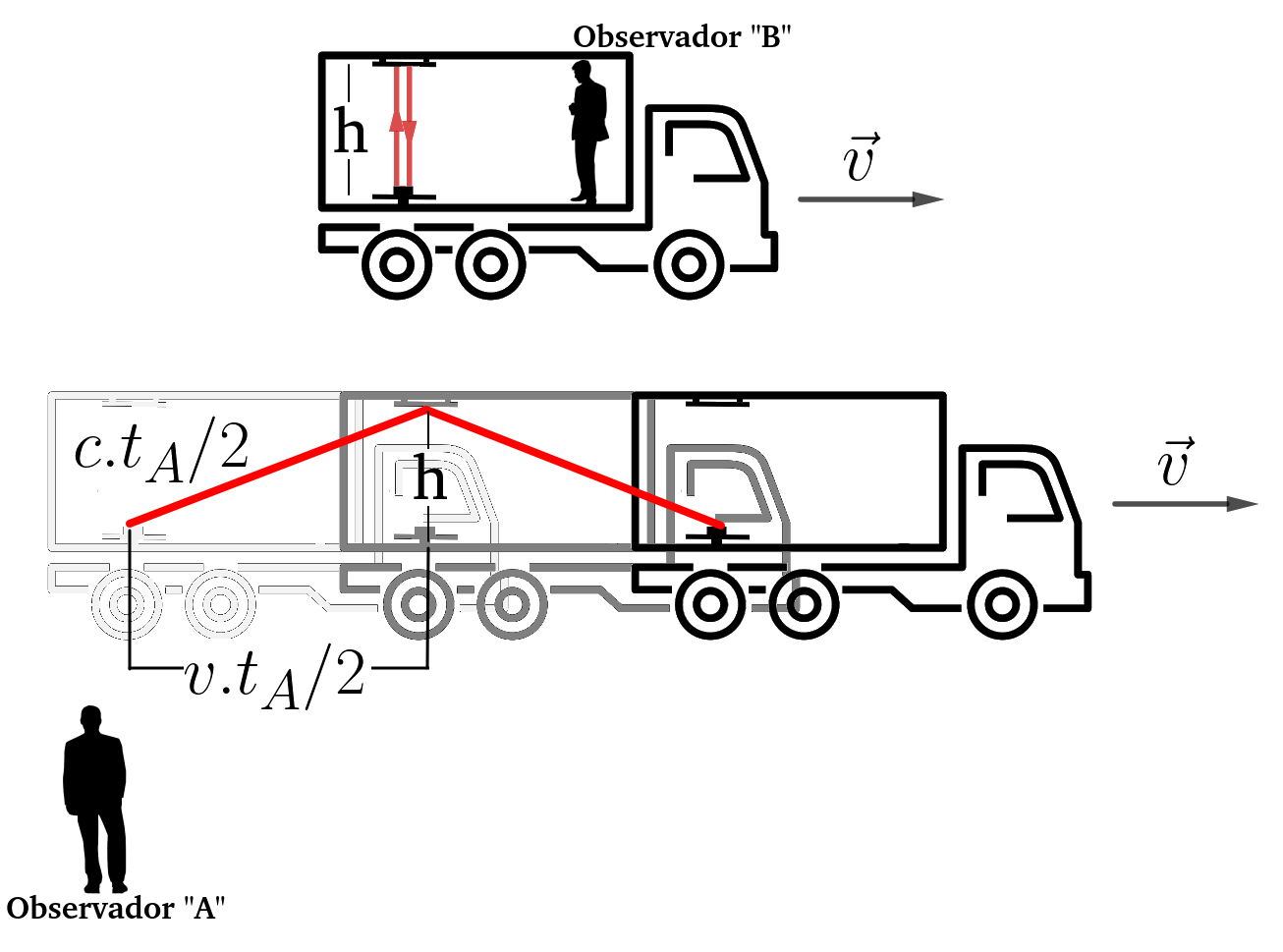
TEMPO DECORRIDO PARA O EVENTO SEGUNDO O OBSERVADOR "A"
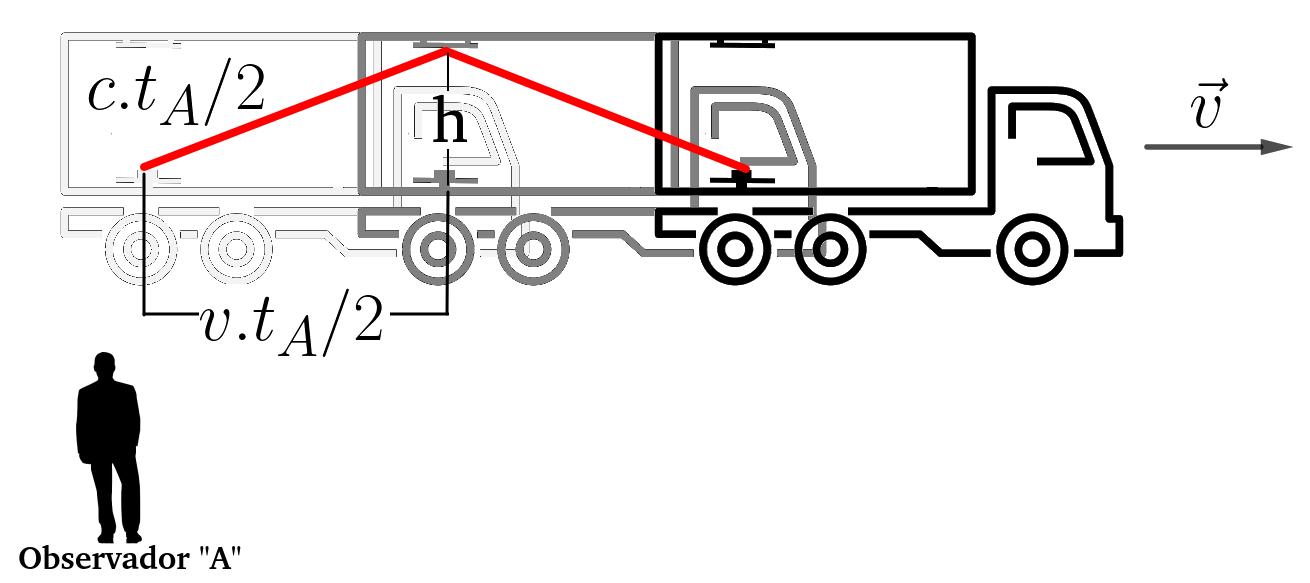
Analizando o triângulo retângulo e aplicando pitágoras, obteremos:
Tempo próprio (t0)
Chamamos de tempo próprio o tempo medido no referêncial em que os eventos que demarcam o intervalo de tempo acontencem no mesmo local.
O tempo próprio sempre será menor ou igual ao tempo não próprio:
Ex.:
|
1) Um ciclo do relógio de luz é demarcado por dois eventos: a emissão do raio luminoso e a recepção deste raio. Observe que no exemplo ao lado, ambos os eventos, tanto a emissão quanto a recepção do raio, acontecem no mesmo local para o observador que está no interior do veículo. Com efeito, o tempo marcado por ele é o tempo próprio. E este tempo será necessariamente menor ou igual (caso o veículo esteja em repouso com respeito ao observador de fora) ao tempo marcado pelo observador de fora. |
|
|
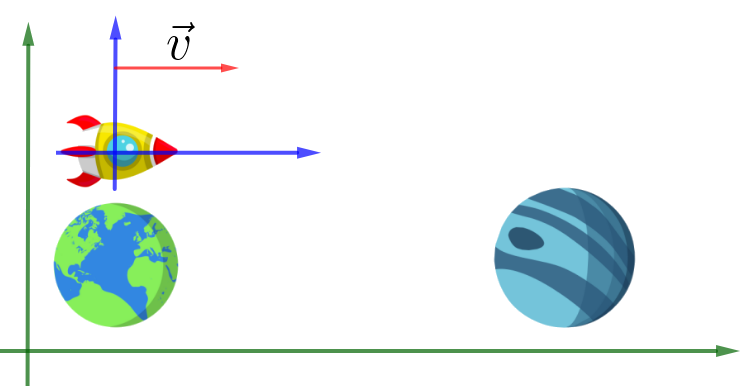
2) Uma nave espacial viaja do planeta Terra até Urano. O tempo de viagem é demarcado por dois eventos: Nave sobre a terra e nave sobre Urano. Observem que estes dois eventos se dão no mesmo lugar no referêncial preso a nave viajante, logo o tempo medido na nave é o tempo próprio. |
|
Contração de Lorentz
Medir comprimentos pressupões que realizemos duas medidas simultaneamente. No entanto, as transformadas de Lorentz dizem que um evento simultâneo em um referêncial pode não ser simultâneo em outro. Para contornar tal situação, mediremos, em cada referêncial, o tempo que o objeto medido demora para passar diante de um determinado ponto. Sabendo-se este tempo e a velocidade entre os referenciais, teremos a medida desejada.
Extraíremos a fórmula que nos permite calcular a medida a partir do exemplo a seguir. O objetivo é calcular o comprimento da nave espacial.
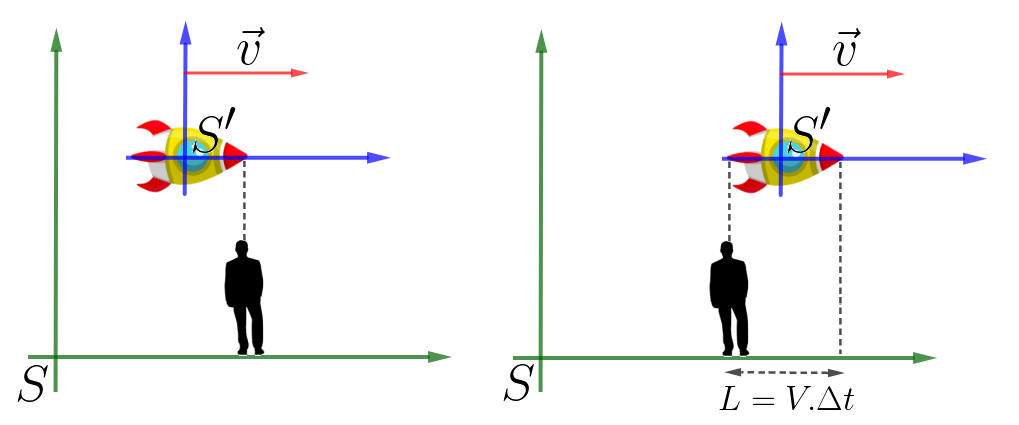
Perceba que o comprimento marcado em S é dado por:
E por analogia podemos medir o comprimento em S' através de:
Sabemos que próprio é o tempo medido em S.
Misturando estas equações, chegaremos na fórmula da contração de Lorentz:
Comprimento próprio (L0).
O comprimento próprio de um objeto é o comprimento tomado no referencial em este objeto encontra-se estático.
Intervalo espaço-temporal (S2)
O intervalo espaço temporal é um quantidade que permanece constante de um referêncial para outro. Para obtermos a relação, analisaremos o seguinte experimento:
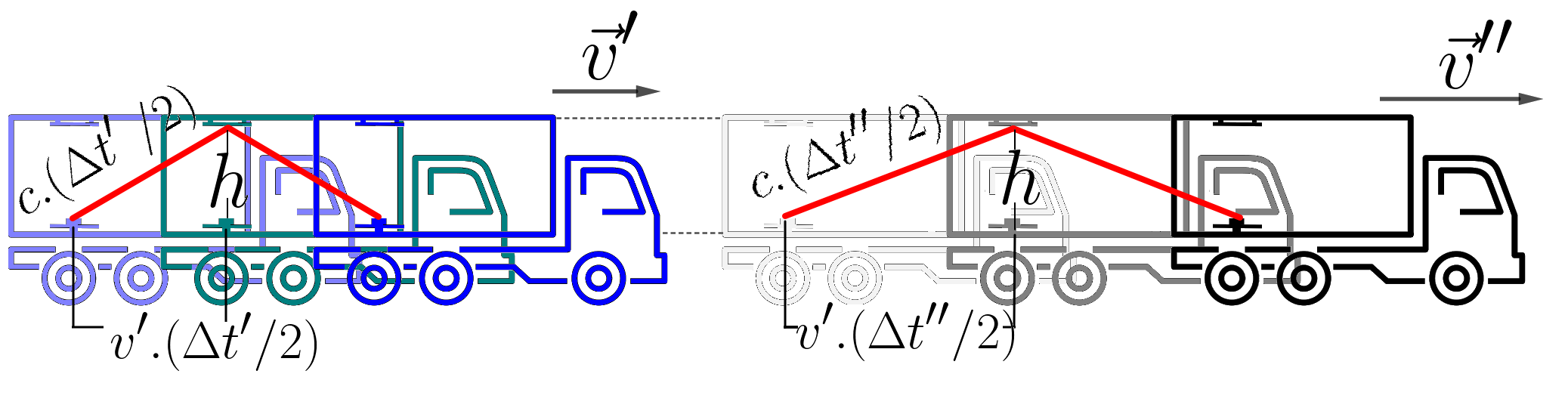
Se escrevermos o teorema de pitágoras para os dois triângulos retângulos destacados, poderemos unir as expressões por intermédio da altura, que é a mesma nos dois casos. Assim, obteremos:
Assim, concluimos que o invariante relativístico é: