Aula
Aula 
Aula 12-96: Momento e energia relativísticos

Momento linear relativístico
Em mecânica clássica, o momento linear de um corpo é um grandeza física cuja definição foi estabelecida visando-se a sua conservação na ausência de força resultante sobre o corpo em questão. Isto é, os físicos constataram que esta quantidade permanecia constante em quaisquer referenciais na ausência de força resultante agindo sobre um determinado corpo e, a esta quantidade, deram o nome de momento linear.
No entanto, em relatividade, a quantidade clássica (que é dada pelo produto massa X velocidade) não se conserva. Neste contexto, uma quantidade que se conserva e que desempenha papel semelhante ao momento linear clássico é o momento linear relativístico.
Energia relativístiva
Analogamente ao que ocorre com o momento linear, acontece com a energia. A energia também é uma grandeza física cuja definição foi estabelecida visando-se a sua conservação em quaisquer refereciais em sistemas conservativos. A energia clássica também não se conserva no contexto da relatividade.
A expressão que nos dá a quantidade que se conserva nestes sistemas, em relatividade, é a seguinte.
Em que a energia de repouso é:
E a energia cinética vale:
Outras quantidades que se apresentam invariantes de um referencial para outro são:
◦ Relação pitagórica da eneriga relativística
◦ Relação triangular da eneriga relativística
O elétron-volt
|
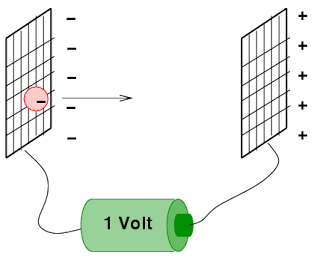
Trata-se de uma unidade de medida muito conveniente para se lidar com quantidades pequenas de energia. Um elétronvolt corresponde ao trabalho necessário para se fazer um elétron atravessar uma barreira de um volt. |
|
Teorema trabalho-energia para relatividade
Em física clássica, aprendemos que a variação de energia cinética de um corpo é igual ao trabalho realizado por ou sobre ele e que, em casos em que há energia potencial, a variação desta energia é igual a menos o trabalho realizado por ou sobre ele. O teorema que descrevia a relação entre a variação de energia cinética e trabalho era chamado teorema trabalho-energia.
Agora, em relatividade, temos algo semelhante. O teorema energia-trabalho para relatividade sustenta que o trabalho realizado por ou sobre um corpo é igual a variação de energia relativística:
Partículas sem massa
É experimentalmente comprovada a existencia de pelo menos uma partícula sem massa na natureza: o fóton. Especula-se que hajam mais: o gráviton, por exemplo. Em termos de física clássica, é impossível se explicar o comportamento destas partículas, mas a relatividade nos dá pistas sobre isto.
Da relação pitagórica, levando-se em consideração a nulidade de massa, obteremos que:
Mirando a relação triangular, constamos que:
Ou seja, disto decorre que partículas sem massa viajam na velocidade da luz.
Com este valor de velocidade, o desta partícula vai ao infinito. Isto gera uma indeterminação no cáculo da energia desta partícula, porquanto
vale infinito e massa vale 0.
Desta breve análise, concluímos que partículas sem massa:
➔ Tem velocidade igual a velocidade da luz c;
➔ Tem energia diferente de zero.