Aula

Lista de Exercícios

Aula 2-18: Aceleração e força centrípeta

Aceleração tangencial e aceleração centrípeta


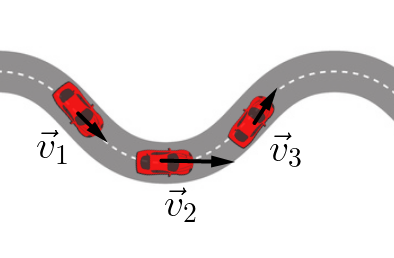
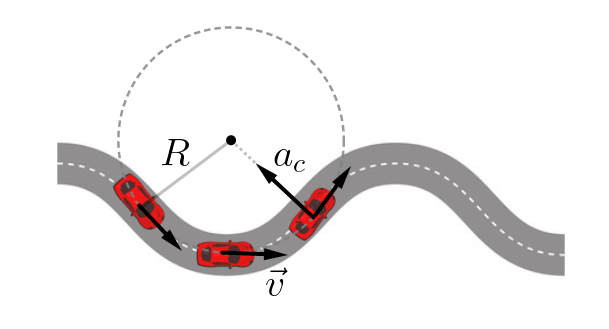
Aprendemos em aulas anteriores que aceleração é uma grandeza física que nos cede informações acerca de como a velocidade varia com o tempo. Naquele contexto, estudamos a aceleração dita tangencial, que dizia respeito a alterações impressas no módulo da velocidade; agora, introduziremos um novo tipo de aceleração, que diz respeito a alterações impressas na direção e sentido da aceleração: a acelração centrípeta. Veja a ilustração ao lado: como o móvel simultaneamente tem a sua velocidade alterada em módulo e em sentido, então simultaneamente está agindo sobre ele a celeração tangencial e a aceleração centrípeta.

Aprendemos em aulas anteriores que aceleração é uma grandeza física que nos cede informações acerca de como a velocidade varia com o tempo. Naquele contexto, estudamos a aceleração dita tangencial, que dizia respeito a alterações impressas no módulo da velocidade; agora, introduziremos um novo tipo de aceleração, que diz respeito a alterações impressas na direção e sentido da aceleração: a acelração centrípeta.

Veja a ilustração ao lado: como o móvel simultaneamente tem a sua velocidade alterada em módulo e em sentido, então simultaneamente está agindo sobre ele a celeração tangencial e a aceleração centrípeta.

Carro virando uma curva, velocidade representada em vetores

➔ ACELERAÇÃO TANGÊNCIAL: A aceleração tangencial é a aceleração que promove alteração no módulo do vetor velocidade. Esta aceleração não é capaz de alterar a direção dele.

A fórmula que nos dará a aceleração tangencial, já a conhecemos de estudos pregressos, é a seguinte:

$a_t = \frac{\Delta v}{\Delta t}$

➔ ACELERAÇÃO CENTRÍPETA: A aceleração centrípeta, diferentemente da aceleração tangencial, não afeta o módulo do vetor velocidade, pois esta aceleração é apenas responsável pela variação da velocidade em sentido e em direção:

E a fórmula que nos dará o módulo da aceleração centrípeta é a seguinte:

$\huge a_c = \frac{v^2}{R}$

Em que

◦ $v$ é a velocidade tangencial do móvel;

◦ $R$ é o raio da circunfêrencia cujo arco é percorrido pelo móvel.

Carro virando uma curva, grandezas físicas representadas em vetores

A MEDIDA DA ACELERAÇÃO CENTRÍPETA: DEMONSTRAÇÃO GEOMÉTRICA

Demonstração:


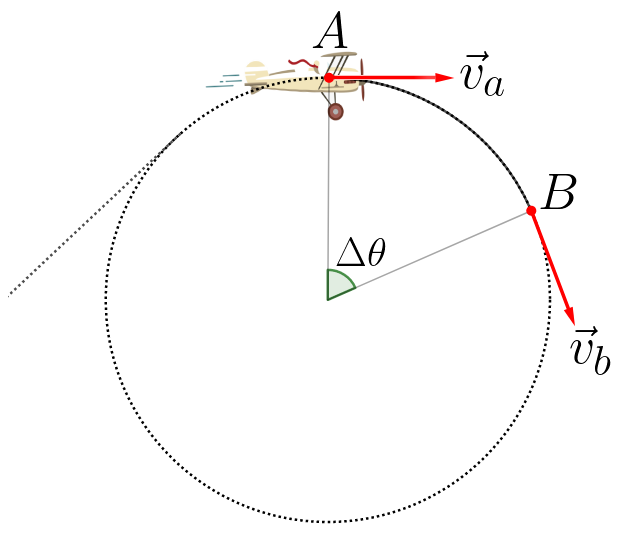
Veja a imagem ao lado, ela é representativa de um móvel que desloca-se em movimento circular uniforme. Ao ir do ponto A ao ponto B, o móvel tem sua velocidade alterada em sentido e direção. Para encontrarmos o valor da aceleração centrípeta 1. Calcularemos a variação de velocidade entre A e B, faremos isto através da subtração do vetor B pelo vetor A; 2. Perceberemos que para ângulos pequenos podemos considerar que o arco de circunfência projeta-se como uma reta, formando um triângulo semelhante ao triângulo primeiro.

Veja a imagem ao lado, ela é representativa de um móvel que desloca-se em movimento circular uniforme. Ao ir do ponto A ao ponto B, o móvel tem sua velocidade alterada em sentido e direção. Para encontrarmos o valor da aceleração centrípeta

1. Calcularemos a variação de velocidade entre A e B, faremos isto através da subtração do vetor B pelo vetor A;

2. Perceberemos que para ângulos pequenos podemos considerar que o arco de circunfência projeta-se como uma reta, formando um triângulo semelhante ao triângulo primeiro.

Avião executando um looping

Avião em lopping com grandezas físicas representadas por vetores

3. Sabemos que podemos escrever a variação angular em função do arco de circunferência:

$\huge \Delta \theta = \frac{\Delta l }{R}$

E então, por semelhança de triângulos, podemos escrever:

$\huge \Delta \theta = \frac{\Delta l }{R} = \frac{\Delta v}{v} \ \rightarrow \$ $\huge \frac{v.t}{R} = \frac{\Delta v}{v} \ \rightarrow \ \frac{v^2}{R} = \frac{\Delta v}{R} \ \rightarrow \$ $\huge a_c = \frac{v^2}{R}$

Força tangencial e força centrípeta

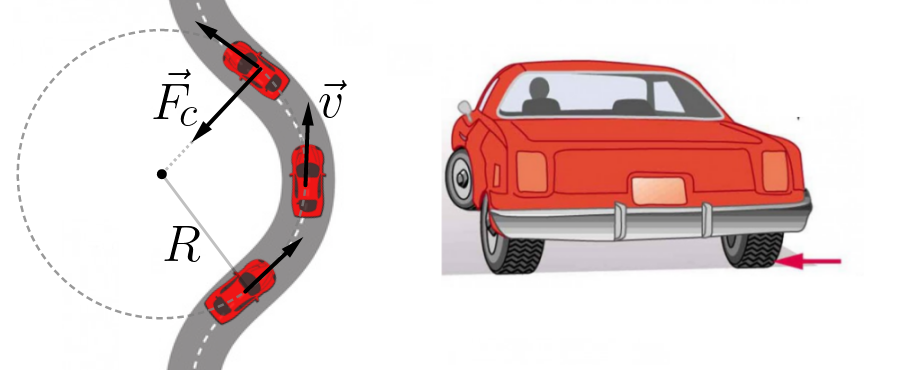
A força tangencial é aquela que imprime no corpo uma aceleração tangencial, ou seja, é a força capaz de alterar o módulo do vetor velocidade deste corpo, não alterando a direção. A força centrípeta é força que é capaz de gerar neste corpo uma alteração na direção do seu vetor velocidade, não alterando a magnitude dele.


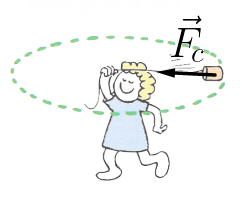
A figura ao lado mostra um corpo de massa m sob o efeito de uma força centrípeta. Observe que a cada instante a direção do vetor velocidade é alterado.

A fórmula que nos dará a força resultante tangencial, já a conhecemos de estudos pregressos, é a seguinte:

$\vec F_r_t = m . \vec a_r_t$

E a fórmula que nos dará a força resultante centrípeta é a seguinte:

$\vec F_r_c = m . \vec a_r_c$

substituindo a aceleração centrípeta teremos:

$\vec F_r_c = \frac{m.v^2}{R}$

Pneu do carro fazendo ele virar uma curva

Tipos de movimentos e suas respectivas acelerações
Movimento		Força / aceleração tangencial	Força / aceleração centrípeta
Retilíneo	Uniforme	Nula	Nula
Retilíneo	Uniformemente variado	Não nula	Nula
Circular	Uniforme	Nula	Não nula
Circular	Uniformemente variado	Não nula	Não nula

A "força" centrífuga

O que chamamos de "força" centrífuga não é, na verdade, propriamente uma força, pois acreditamos que tal fenômeno não se trata de uma interação entre dois corpos, mas, sim, uma manifestação do princípio da inércia: Quando colocamos algo para girar em movimento circular, fazemos isto mediante a aplicação de uma força centrípeta. Caso esta força deixe de existir, os corpos tenderão a manter sua trajetória retílinea, saindo pela tangente. Quando isto acontece, tem-se a impressão de que está sendo arremeçado para "fora". E a este arremeço é dado o nome de "força" centrípeta.

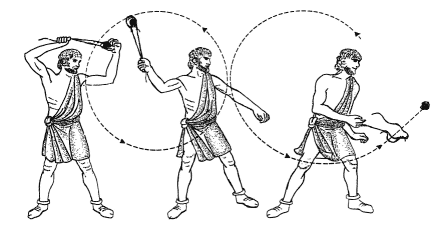
A funda de Davi

Segundo os relatos bíblicos, o jovem Davi, futuro rei de Israel, amparado por uma funda, derrotou em combate o gigante Golias.

Uma funda é um armamento que consiste em uma correia dobrada em cujo centro deposita-se um projétil. Ao girar-se a correia, o projétil, forçado pela tensão da haste, move-se circularmente. Ao liberar-se uma das extremidades da correia, a força centrípeta deixa de existir e o projétil é "disparado" pela tangente.

Representação do método de funcionamento de uma funda

A máquina de secar roupas

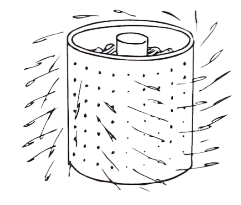
Desenho de maquina centrifuga expelindo água

As paredes destas máquinas são projetadas de modo a compelir as roupas ao movimento circular, ao passo que a água não. A água é, portanto, ejetada pelos poros das paredes.

Colônias espaciais

Construir uma nave espacial que, assemelhando-se a um pneu, execute um movimento circular uniforme é uma maneira de se viabilizar a simulação de gravidade:

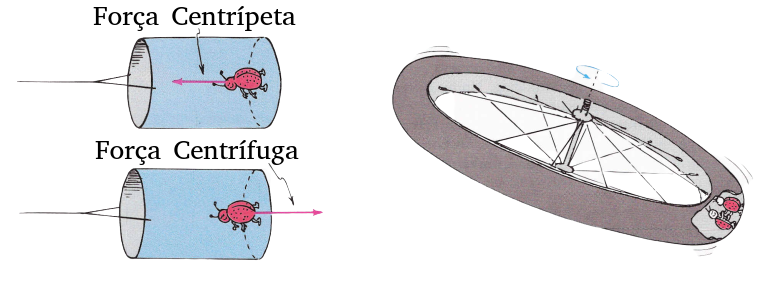
Desenho de uma pneu com seres vivos dentro vivendo em uma gravidade simulada

A ficção científica dos filmes 2001 - Uma Odisseia no Espaço, de 1969, e Interstelar, de 2014, faz uso de ideias semelhantes para a contrução de colônias espaciais.

Arte que representa uma colônia espacial