Aula
Aula 
Aula 2-19: Trabalho

Trabalho é a energia transferida (fornecida ou retirada) a um corpo mediante a aplicação de uma força no decorrer de uma trajetória.
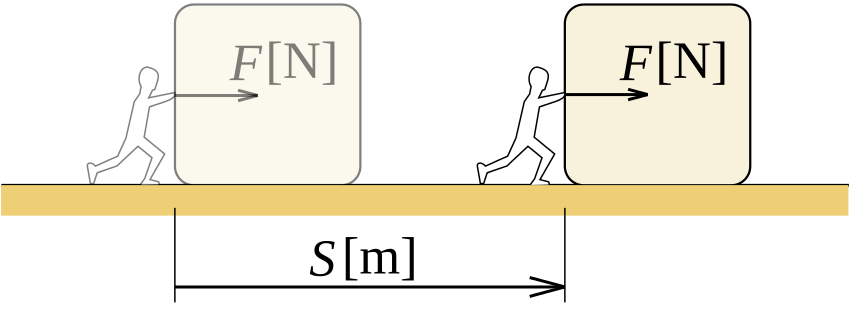
Da definição apresentada, infere-se que o trabalho é proporcional a trajetória do corpo na direção da força (pois quanto maior ela for, mais energia será transferida); infere-se, também, que o trabalho é proporcional à magnitude da força (pois a energia transferida será maior na medida em que a força aplicada é maior). Podemos, portanto, escrever:
$${ W = F . d }$$
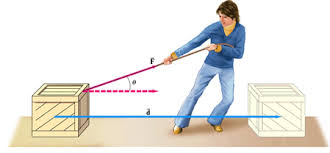
Na figura acima, a força é aplicada na direção do movimento e, logo, a fórmula já citada é válida. No entanto, pode haver situações (observe a figura abaixo) em que a força aplicada não está direcionada conforme o percurso do objeto estudado, devemos, então, decompor a força e substituir na fórmula apenas a componente desejada (a componente cuja direção é igual a direção do deslocamento). Ao se fazer isto, obteremos a seguinte expressão:
$${ W = F . d . cos(\theta) }$$
⚛ CLASSIFICAÇÃO:
Quando a força aplicada sobre o objeto se projeta no mesmo sentido do seu deslocamento, este trabalho é positivo, pois , e o chamamos de trabalho motor. Quando a força aplicada se projeta em sentido oposto, o trabalho será negativo, pois, e o chamamos de trabalho resistente.

Trabalho da força peso
|
|
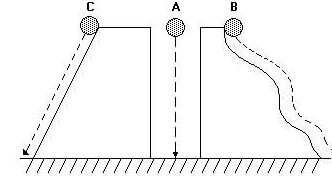
Em situações convencionais, a força peso age verticalmente, logo não haverá trabalho da força peso quando o corpo se deslocar horizontalmente. Quando ocorre deslocamento vertical, haverá trabalho da força peso e esta não dependerá do trajeto, mas apenas da posição inicial e final. |
Trabalho da força resultante centrípeta
|
|
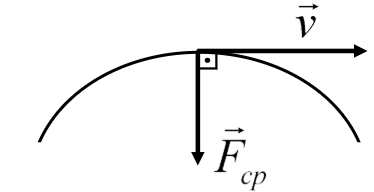
O trabalho da força centrípeta é sempre nulo! Observe que esta força sempre atua na direção perpendicular à direção de deslocamento do objeto analisado, portanto não pode haver trabalho nessa situação. |
Trabalho da força resultante elástica
|
|
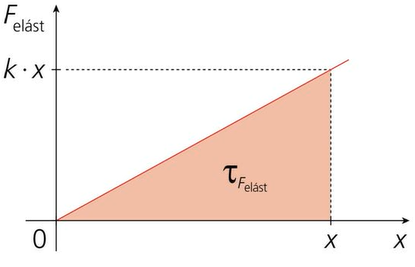
Ao plotarmos um gráfico da força pela distância, temos que a área dele é numericamente igual ao trabalho desta força ao longo do trajeto representado. Podemos ver no gráfico acima, que a área abaixo dele forma um triângulo retângulo. Podemos, portanto, calcular a sua área, já que ela é igual ao produto dos catetos dividido pela metade. Temos, então, que o trabalho da força elástica é: |