Aula

Lista de Exercícios

Aula 3-28: Lei da gravitação universal


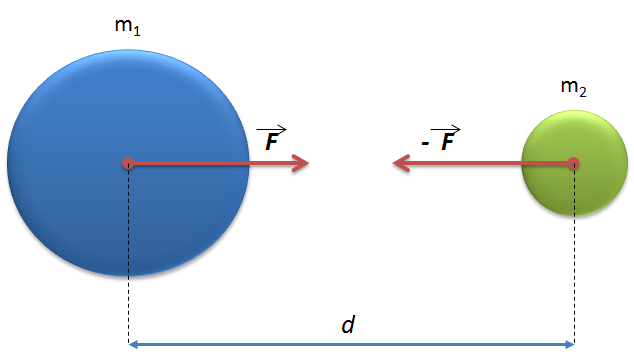
Enunciado: Dois corpos atraem-se por forças de módulo diretamente proporcional as suas massas e inversamente proporcional ao quadrado da distância que os separam. Essa força é denominada gravitacional e, em caso de corpos puntiformes, ela age na direção de uma reta que os traspassa pelo centro. $F = \frac{G .m_1 . m_2 }{d^2}$ Em que G = 6,67.10-11 N.Kg²/m²

Enunciado:

Dois corpos atraem-se por forças de módulo diretamente proporcional as suas massas e inversamente proporcional ao quadrado da distância que os separam. Essa força é denominada gravitacional e, em caso de corpos puntiformes, ela age na direção de uma reta que os traspassa pelo centro.

$F = \frac{G .m_1 . m_2 }{d^2}$

Em que G = 6,67.10-11 N.Kg²/m²

Dois corpos massivos se atraindo mutuamente de acordo com a lei da gravitação universal

Princípio da superposição

Quando há dois corpos massivos, redondos e de constituição homogênica, a força que atuará nestes corpos é na direção de uma linha que os une pelo centro (veja a primeira imagem acima). Entretanto, quando há mais de dois corpos envolvidos no problema, devemos calcular a direção da força levando em conta o princípio da superposição. Este princípio afirma que a força resultante sobre o corpo analisado é a soma vetorial das forças oriundas de cada um dos corpos do sistema.

Massa x aceleração


Um fato físico que depõe contra a nossa intuição é que independentemente da massa de um corpo, ele sempre precipita em direção a terra (na verdade, qualquer outro corpo com massa grande o suficiente para atraí-lo) com aceleração constante. Isso significa dizer que se pusermos dois objetos, lado a lado, numa mesma altura – de massas iguais ou radicalmente distintas –, e desprezando o atrito atmosférico, eles chegarão ao solo dentro do mesmo intervalo de tempo. O que explica este fenômeno é equivalência existente entre massa gravitacional e massa inercia. Veja a relação:

Um fato físico que depõe contra a nossa intuição é que independentemente da massa de um corpo, ele sempre precipita em direção a terra (na verdade, qualquer outro corpo com massa grande o suficiente para atraí-lo) com aceleração constante. Isso significa dizer que se pusermos dois objetos, lado a lado, numa mesma altura – de massas iguais ou radicalmente distintas –, e desprezando o atrito atmosférico, eles chegarão ao solo dentro do mesmo intervalo de tempo.

O que explica este fenômeno é equivalência existente entre massa gravitacional e massa inercia. Veja a relação:

Dois corpos são abandonados simultaneamente do alta da torre de pisa

$P = F_g \rightarrow m_i_1 . g = \frac{G . m_g_1 . m_g_2}{d^2}$ $\rightarrow g = \frac{G . m_g_2}{d^2}=constante$

Gráfico força gravitacional X distância

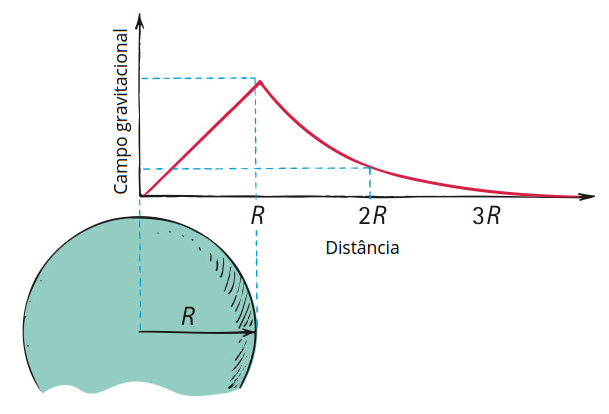
Gráfico da força gravitacional em função da distância interna e externa ao corpo

É possível, através de uma matemática de nível avançado, demonstrar que a força gravitacional no interior do planeta terra cresce linearmente com a distância do centro de massa da terra, e, externamente ao planeta, como é evidenciado pela lei da gravitação universal, a força cai com o quadrado da distância. Observe a representação:

Demonstração da terceira lei de Kepler

Lembremo-nos, antes, da terceira lei de Kepler (Lei dos períodos): A razão entre o quadrado do período orbital de um planeta e seu raio é constante (constante de Kepler):

$\frac{T_a^2}{R_a^3}=\frac{T_b^2}{R_b^3}=\frac{T_n^2}{T_n^3}=K$


Sabemos, pois, que a resultante centrípeta que faz com que um corpo celeste orbite outro corpo é a própria força gravitacional, então: $F_c = F_g \rightarrow m_1.\omega^2.R = \frac{G.m_1.m_2}{R^2}$ $\rightarrow (\frac{2.\pi}{T})^2 .R= \frac{G.m_2}{R^2}$ $\rightarrow \frac{T^2}{R^3}= \frac{4.\pi^2}{G.m_2}=K$

Sabemos, pois, que a resultante centrípeta que faz com que um corpo celeste orbite outro corpo é a própria força gravitacional, então:

$F_c = F_g \rightarrow m_1.\omega^2.R = \frac{G.m_1.m_2}{R^2}$ $\rightarrow (\frac{2.\pi}{T})^2 .R= \frac{G.m_2}{R^2}$ $\rightarrow \frac{T^2}{R^3}= \frac{4.\pi^2}{G.m_2}=K$

O sol atraindo a Terra

Experimento de Cavendish

Em 1798, o físico inglês Henry Cavendish (★ 1731 — 1810 ✝) calculou, pela primeira vez, o valor aproximado da constante gravitacional G. Para cumprir tal façanha, usou uma balança de torção, conforme mostra a ilustração abaixo:

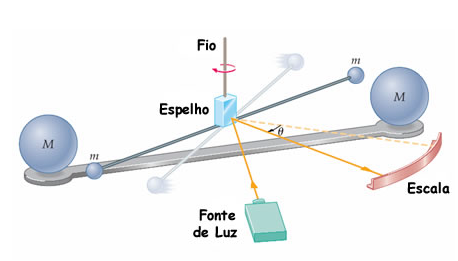
representação da balança de torçao usada por Cavendish para definir o valor da constante gravitacional

A balança era formada por um eixo delgado que conectava duas esferas maciças. Este eixo era sustentado por um fio portador de um espelho que refletia um feixe de luz. Fazendo uso deste equipamento, o cientista aproximou duas outras esferas maciças daquelas que eram suspensas pelo fio. Após fazer isso, como era esperado, o fio moveu-se (devido a força gravitacional) e, por conseguinte, a angulação do feixe de luz refletido se alterou. O cientista, munido dos dados que obtivera, realizou os cálculos necessários e encontrou o valor da constante gravitacional G.