Aula
Aula 
Aula 4-30: Introdução à estática

Estática é o setor da física que se ocupa do estudo de situações que dialogam fortemente com o conceito de equilíbrio mecânico estático.
Ponto material e corpo extenso
Ao estudarmos um corpo, podemos classificá-lo em dois grupos:
-
Ponto material: ponto material é nome dado ao ponto imaginário que usamos para substituir um corpo qualquer. podemos fazer isso sempre que as dimensões do corpo forem desprezíveis para a resolução do problema.
-
Corpo extenso: Corpo extenso é o nome dado ao corpo cujas dimensões não podem ser desprezadas para efeito de cálculo.
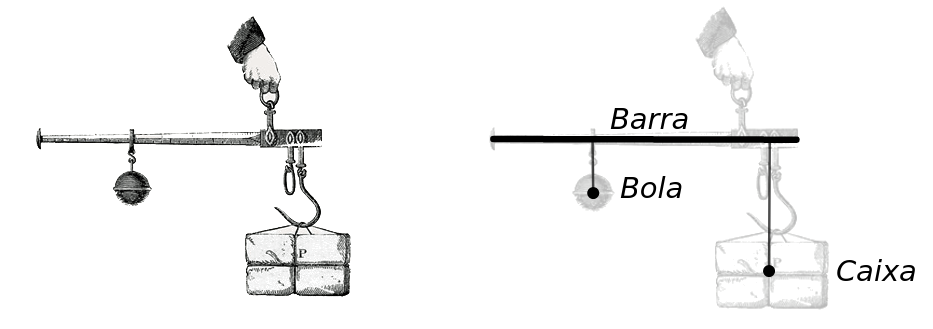
Na imagem abaixo temos um sistema mecânico (balança romana) em que se equilibram uma bola e uma caixa. Em breve veremos que, para explicar perfeitamente os fatos em questão, não precisamos levar em consideração as dimensões da bola e da caixa, e que, portanto, podemos substituí-las por um ponto no diagrama. Tais objetos, bola e caixa, são, pois, neste caso, pontos materiais.
Agora, em se tratando da barra, é diferente. Neste caso, o seu comprimento é relevante para a explicação do fenômeno; portanto a barra é classificada como corpo extenso.
Equilíbrio de um ponto material
O equilíbrio de um ponto material ocorre sempre que a força resultante sobre ele é nula. Para nos certificarmos de que isto ocorre, devemos percorrer os passos arrolados abaixo:
I. Primeiramente, coloquemos o problema num diagrama da forma mais simplificada possível, desenhando todas as forças relevantes que agem sobre o ponto material
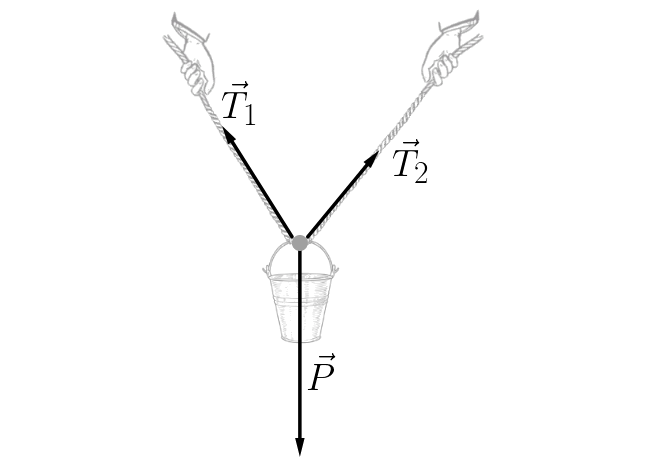
II. Escolher um sistema de refêrencia conveniente. Geralmente um sistema de eixos horizontal e vertical é uma boa escolha. Após isto, devemos decompor as forças de modo a projetá-las sobre estes eixos.
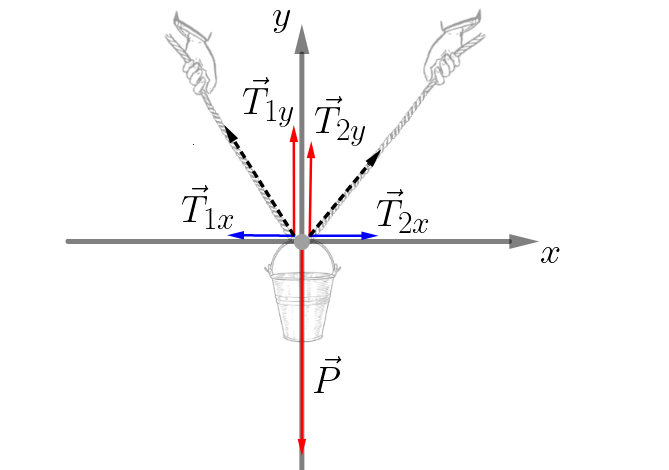
III. De último, basta que analisemos o problema em cada eixo. Para haver equilíbrio, a somatória das forças deve resultar em zero.
EIXO Y
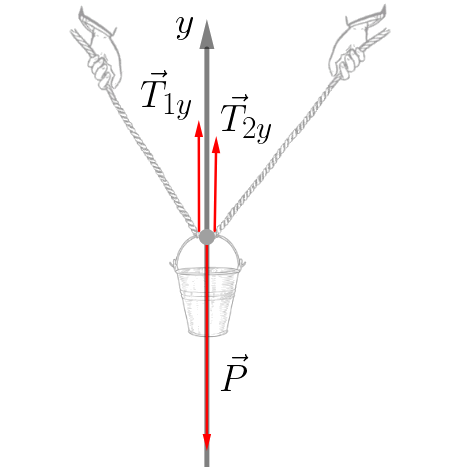
Para haver o equilíbrio destas forças, a soma das forças que agem pra cima devem ser, em módulo, igual a soma das forças que agem para baixo:
EIXO X
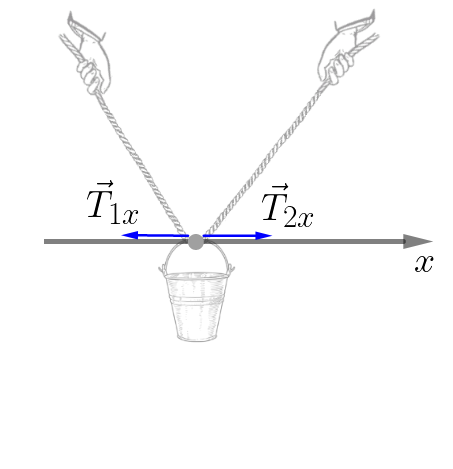
Para haver o equilíbrio destas forças, a soma das forças que agem pra cima devem ser, em módulo, igual a soma das forças que agem para baixo:
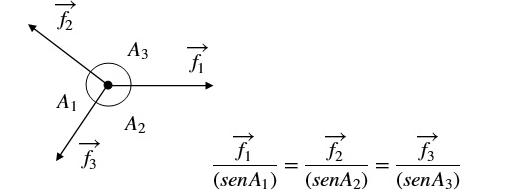
Teorema das três forças
Este teorema afirma que toda vez que um corpo se encontra em equilíbrio estático (translacional e rotacional) e sob ação exclusiva de três forças, então estas forças estão em direções paralelas entre si ou são concorrentes a um ponto.
Teorema de Lamy
É um teorema de grande utilidade na resolução de problemas de estática, pois quando um ponto material está em equilíbrio e submetido à ação de três forças coplanares (num mesmo plano) e concorrentes (as direções se encontram num mesmo ponto), o teorema diz que a razão entre o módulo de cada força e o seno do ângulo oposto é constante.