Aula 6-47: Trabalho nas transformações gasosas

Trabalho nas transformações isobáricas

 

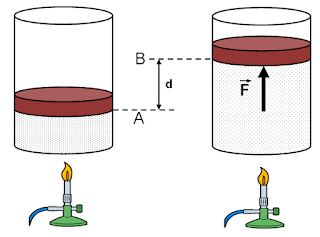
A figura ao lado exibi um recipiente contendo gás e isolado por um êmbolo. Quando o recipiente é aquecido, o embolo se move fazendo com que o seu volume aumente e que a pressão no seu interior permaneça constante. O trabalho é, como sabemos, dado pela expressão: observe que, neste caso, a força coincide em direção e sentido com o sentido de deslocamento do êmbolo, o que faz resultar num ângulo igual a 1.

Podemos multiplicar, neste caso, a equação do trabalho por um fator que vale 1 sem alterá-la; e, assim, obteremos:

Como a pressão é constante, ao se variar o volume, o trabalho será dado pela expressão:

 

➔ CLASSIFICAÇÃO DO TRABALHO: O trabalho realizado pelo gás na representação acima é positivo, entretanto, se, durante este processo, a força se opuser ao sentido de percurso do êmbolo (isso acontece quanto ocorre um deslocamento negativo), então o ângulo equivaleria a -1, resultando num trabalho negativo.

Movimento	Volume	Trabalho	Sinal
Expansão	Aumenta	Motor	Positivo
Compressão	Diminui	Resistente	Negativo
Nenhum	Constante	Inexistente	Inexistente

➔ OUTRO MODO DE SE FORMULAR O TRABALHO

A equação de Clapeyron nos informa que . Como estamos estudando situações em que a pressão é constante, então podemos inferir que, já que todo o mais é constante, o seguinte é verdade:

 

➔ GRÁFICO PRESSÃO X VOLUME

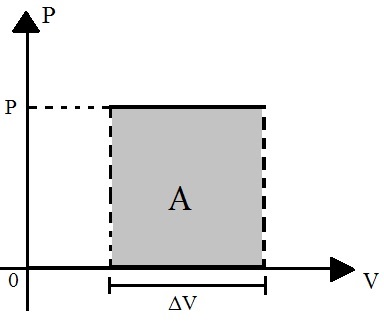		A área do gráfico (Pressão x volume) é numericamente igual ao trabalho realizado por um gás durante a variação de volume. E isto vale para qualquer tipo de transformação.

 

 

Trabalho em transformações isotérmicas

Como sabemos, pela lei de Boyle, numa transformação isotérmica pressão e volume são inversamente proporcionais, portanto, se um aumenta, o outro diminui. Abaixo temos o gráfico Pressão X volume duma expansão isotérmica:

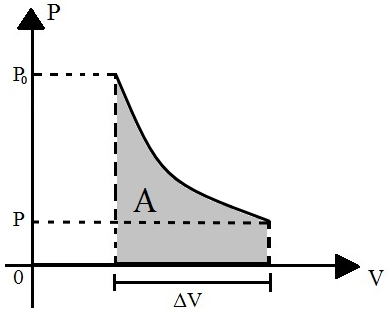		Podemos, então, a partir deste gráfico, obter o trabalho do gás nesta transformação, calculando a área destacada. Como o cálculo desta área não é trivial, não o realizamos no ensino médio, embora o cálculo seja possível através de ferramentas matemáticas avançadas.

 

 

Trabalho em transformações isovolumétricas

 

Como neste tipos de transformação não há variação de volume, logo não há trabalho, pois para haver trabalho é imprescindível que o gás desloque uma fronteira.

 

 

Trabalho em transformações adiabáticas

 

Veremos como calculá-lo na aula seguinte, após travarmos contato com a primeira lei da termodinâmica.

 

 

Trabalho em transformações cíclicas

 

Igualmente, o trabalho é numericamente igual a área do gráfico:

 

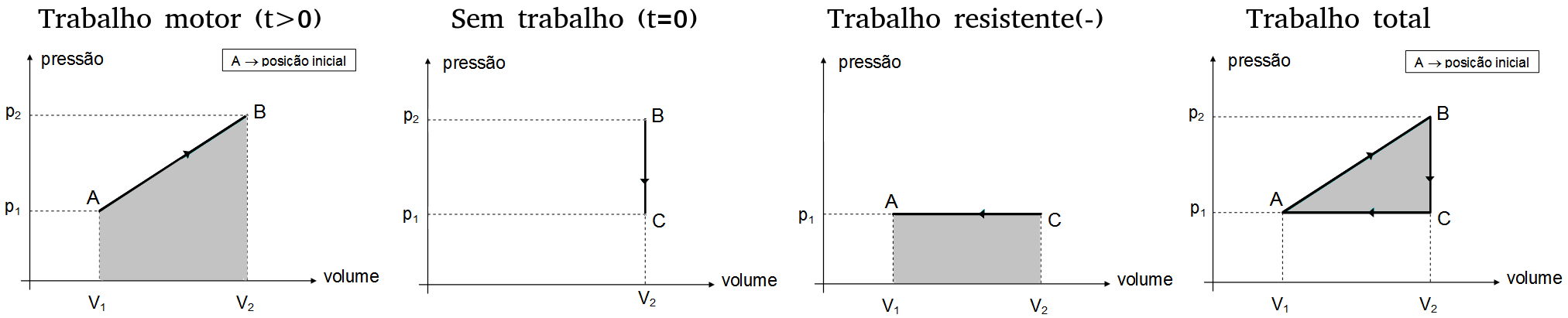
Observe que, o trabalho total de um ciclo é igual a soma dos trabalhos provenientes de todas as variações de volume.