Aula

Lista de Exercícios

Aula 8-67: Ondas estacionárias


São ondas que, sofrendo concomitantemente os fenômenos da reflexão e interferência, formam um padrão de vibração estático. Estudaremos, aqui, ondas estacionárias em cordas e em tubos.

Ondas estacionárias em cordas


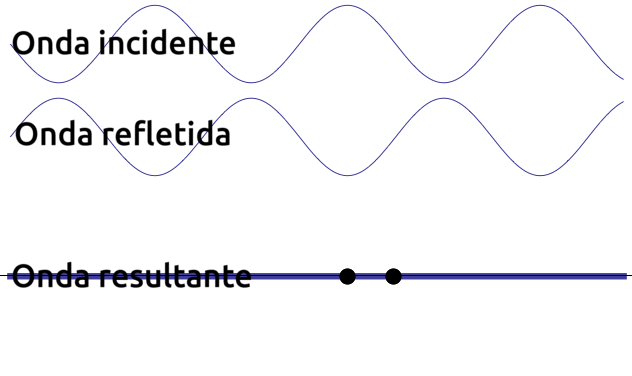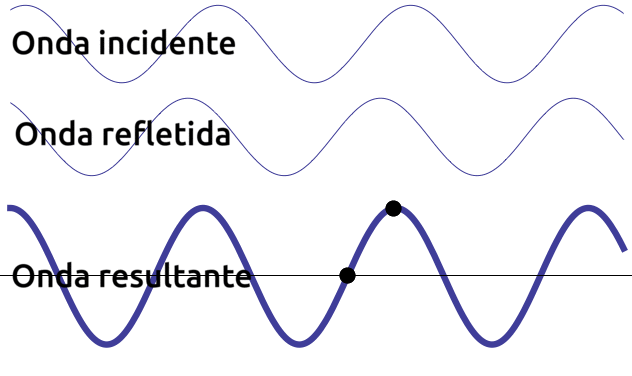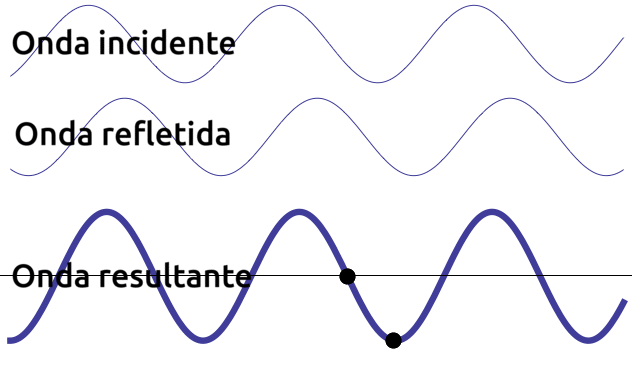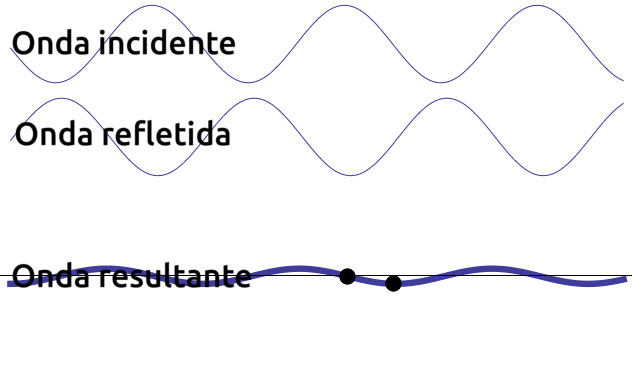
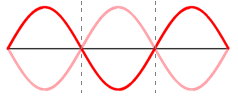
	A imagem ao lado ilustra uma onda que incide ininterruptamente sobre um anteparo refletor (não ilustrado) que gera ininterruptamente uma onda refletida. A onda progressiva (incidente) e a onda regressiva (refletiva) se somam pelo princípio da superposição de ondas formando um padrão de onda estacionário.
	Nó: ponto da onda que, durante a sua oscilação, permanece imóvel; Antinó: ponto que se move com a maior amplitude possível; Ventre: Região contida entre dos nós adjacentes; Modo de vibração: indica quantos ventres existem na onda.

A imagem ao lado ilustra uma onda que incide ininterruptamente sobre um anteparo refletor (não ilustrado) que gera ininterruptamente uma onda refletida. A onda progressiva (incidente) e a onda regressiva (refletiva) se somam pelo princípio da superposição de ondas formando um padrão de onda estacionário.

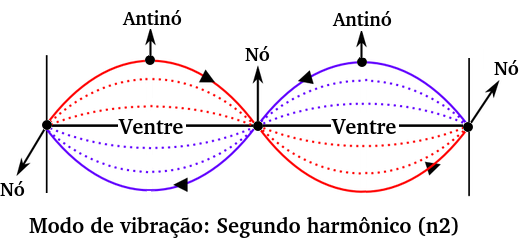
Nó: ponto da onda que, durante a sua oscilação, permanece imóvel;

Antinó: ponto que se move com a maior amplitude possível;

Ventre: Região contida entre dos nós adjacentes;

Modo de vibração: indica quantos ventres existem na onda.

➔ RELAÇÃO ENTRE COMPRIMENTO DE CORDA (l), FREQUÊNCIA (f) E MODOS DE VIBRAÇÃO (n)

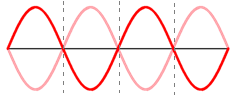
Observe que, analisando as figuras, é possível se extrair as seguintes relações entre os supracitados parâmetros:

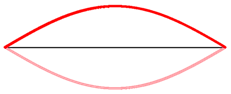
⚛ Harmônico fundamental

(n1)

$l = (1).\frac{\lambda}{2}$

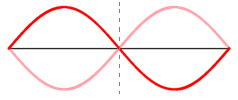
⚛ Segundo harmônico

(n2)

$l = (2).\frac{\lambda}{2}$

⚛ Terceiro harmônico

(n3)

$l = (3).\frac{\lambda}{2}$

⚛ Quarto harmônico

(n4)

$l = (4).\frac{\lambda}{2}$

Relação extraída:

$l = (n).\frac{\lambda}{2}\rightarrow \lambda = \frac{2.l}{n}$ , substituindo na equação fundamental da ondulatória…

$v=\lambda . f\rightarrow v = (\frac{2.l}{n}).f\rightarrow$ $f = n(\frac{v}{2.l})$

➔ APLICAÇÕES DE ONDAS ESTACIONÁRIAS EM CORDAS

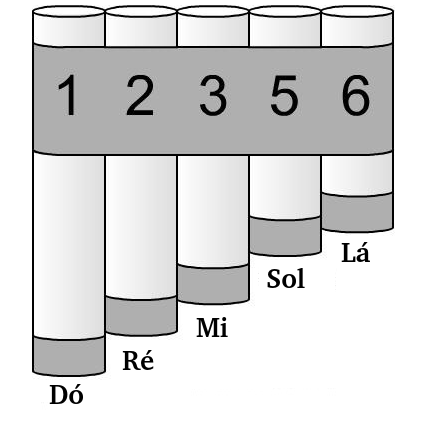
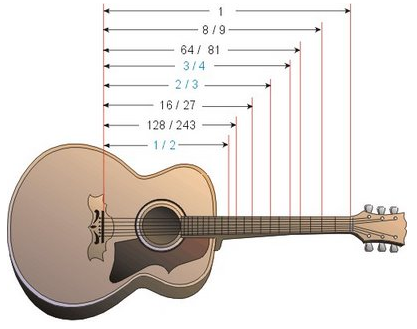
O conhecimento de ondas estacionários é amplamente explorado na ciência musical, pois os instrumentos de corda são projetados levando em consideração estes estudos. Como por exemplo, no caso do violão, o comprimento do braço, a disposição de trastes, a densidade e tração nas cordas, relacionam-se de modo a formar harmônicos específicos, que geram sons mais agradáveis aos nossos ouvidos.

Ondas estacionárias em tubos

O fenômeno é exatamente o mesmo estudado para ondas estacionárias em cordas, o que o torna particular é o fato de que, em se tratando de tubos fechados, não se pode gerar todos os harmônicos que são gerados em cordas.

Ondas estacionárias em tubos abertos: Neste caso, com tubo de extremidades abertas, pode-se, assim como nas cordas, obter-se qualquer harmônico. Veja a análise abaixo.

➔ RELAÇÃO ENTRE COMPRIMENTO DE CORDA (l), FREQUÊNCIA (f) E MODOS DE VIBRAÇÃO (n)

Observe que, analisando as figuras, é possível se extrair as seguintes relações entre os dois parâmetros:

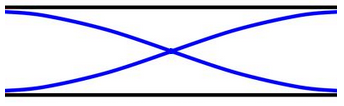
⚛ Harmônico fundamental

(n1)

$l = (1).\frac{\lambda}{2}$

⚛ Segundo harmônico

(n2)

$l = (2).\frac{\lambda}{2}$

⚛ Terceiro harmônico

(n3)

$l = (3).\frac{\lambda}{2}$

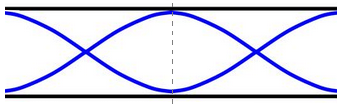
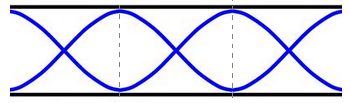
Observe que as relações extraídas para os tubos abertos são idênticas àquelas auferidas para cordas, logo as consequências serão, também, as mesmas:

$l = (n).\frac{\lambda}{2}\rightarrow \lambda = \frac{2.l}{n}$ , substituindo na equação fundamental da ondulatória…

$v=\lambda . f\rightarrow v = (\frac{2.l}{n}).f\rightarrow$ $f = n(\frac{v}{2.l})$

Ondas estacionárias em tubos fechados: Neste caso, com tubo de uma extremidade fechada, diferentemente das cordas e dos tubos de extremidades abertas, não se pode obter qualquer harmônicos; mas só os ímpares. Veja a análise abaixo.

➔ RELAÇÃO ENTRE COMPRIMENTO DE CORDA (l), FREQUÊNCIA (f) E MODOS DE VIBRAÇÃO (n)

Diferentemente das cordas, em que eram permitidos qualquer harmônico (n podia ser qualquer valor real: n1, n2, n3, n4…), com tubos de extremidade fechada só se pode obter harmônicos impares (n1, n3, n5, n7...), observe o esquema abaixo:

⚛ Harmônico fundamental

(n1)

$l = (1).\frac{\lambda}{4}$

⚛ Segundo harmônico

(n2)

$l = (3).\frac{\lambda}{4}$

⚛ Terceiro harmônico

(n3)

$l = (4).\frac{\lambda}{4}$

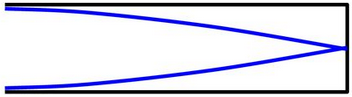
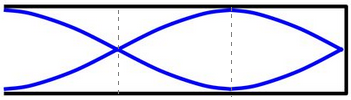
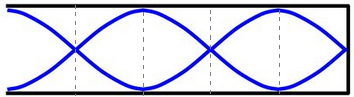
Relação extraída:

$l = (n).\frac{\lambda}{4}\rightarrow \lambda = \frac{4.l}{n}$ , substituindo na equação fundamental da ondulatória…

$v=\lambda . f\rightarrow v = (\frac{4.l}{n}).f\rightarrow$ $f = n(\frac{v}{4.l})$

➔ APLICAÇÕES DE ONDAS ESTACIONÁRIAS EM TUBOS

As aplicações mais notórias de ondas estacionária em tubos também são as que encontramos no âmbito musical, nos metais, instrumentos de sopro.