Aula

Lista de Exercícios

Aula 2-25: Colisões

Colisões são interações entre dois ou mais corpos em que, geralmente, há a atuação de grandes forças em curtos intervalos de tempo. As colisões, por vezes, também são chamadas de choques mecânicos.

Podemos dividir uma colisão em estágios, correspondentes ao período anterior, durante e depois da colisão. Neste processo, é importante ressaltar que o momentum linear sempre se conservará, isto é, o momentum linear antes, durante e depois da colisão permanece o mesmo. Diferentemente do que ocorre com o momentum, a enercia cinética poderá ou não se conservar: caso ela se conserve, temos um caso de colisão perfeitamente elástica; se a energia cinética se conservar parcialmente, então teremos um caso de colisão parcialmente elástica; caso a energia se perca totalmente, indo a zero, então teremos um caso de colisão inelástica.

➔ COEFICIENTE DE RESTITUIÇÃO

Trata-se de um valor obtido a partir da razão entre os módulos da velocidade relativa de aproximação dos corpos (antes do choque) e da velocidade relativa de afastamento dos corpos. Este coeficiente, indiretamente, é indicador da quantidade de energia cinética que se conservará nesta colisão. Ele estará entre 0 e 1; quanto mais próximo estiver de 1, maior será a energia cinética conservada no sistema.


	Observe que como para haver colisão é preciso que a velocidade de "a" seja superior de a "b", então a velocidade relativa de aproximação será dada por: $v_a_p=v_a_0 -v_b_0$ Por argumento análogo, calculamos a velocidade relativa de afastamento através da expressão: $v_a_f=v_a -v_b$

Observe que como para haver colisão é preciso que a velocidade de "a" seja superior de a "b", então a velocidade relativa de aproximação será dada por:

$v_a_p=v_a_0 -v_b_0$

Por argumento análogo, calculamos a velocidade relativa de afastamento através da expressão:

$v_a_f=v_a -v_b$

$e = \frac{|v_a_f|}{|v_a_p|}=\frac{|v_b - v_a|}{|v_a_0 - v_b_0|}$

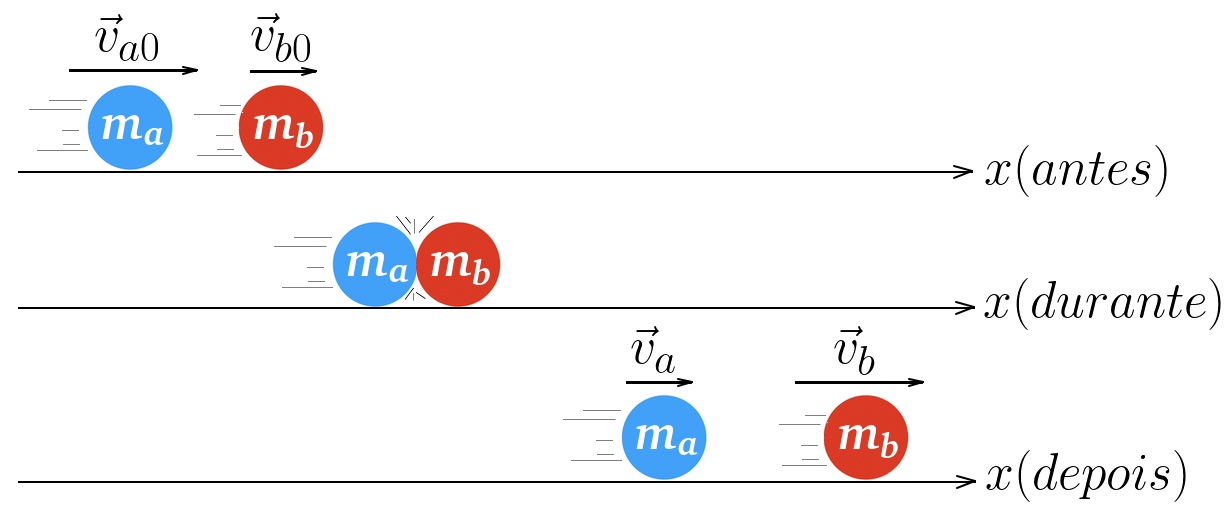
Colisões perfeitamente elásticas

Neste tipo de colisão, por um instante, no momento em que os corpos se tocarem, eles aglutinar-se-ão transformando parte da energia cinética envolvida no sistema em energia potencial e, em seguida, esta energia potencial será totalmente restuida aos corpos, conservando, então, a energia cinética antes e depois do choque.

➔ COEFICIENTE DE RESTITUIÇÃO PARA COLISÕES PERFEITAMENTE ELÁSTICAS

Sempre que estivermos diante de uma colisão perfeitamente elástica, o coeficiente de restituição valerá:

$e = \frac{|v_a_f|}{|v_a_p|}=1$

➔ EQUAÇÃO DAS VELOCIDADES FINAIS PARA COLISÕES ELÁSTICAS

$v_a = (\frac{m_a-m_b}{m_a_+m_b}).v_a_0+(\frac{2.m_b}{m_a+m_b}).v_b_0$

$v_b = (\frac{2.m_a}{m_a+m_b}).v_a_0+(\frac{m_b-m_a}{m_a+m_b}).v_b_0$

$v_a = (\frac{m_a-m_b}{m_a_+m_b}).v_a_0+(\frac{2.m_b}{m_a+m_b}).v_b_0$

$v_b = (\frac{2.m_a}{m_a+m_b}).v_a_0+(\frac{m_b-m_a}{m_a+m_b}).v_b_0$

MEDIDA DO COEFICIENTE DE RESTITUIÇÃO - COLISÕES ELÁSTICAS: DEMONSTRAÇÃO

Considerando que o momentum linear se conserva, podemos escrever:

$Q_0 = Q \ \rightarrow \ m_a.v_a_0+m_b.v_b_0$ $=m_a.v_a+m_b.v_b$ eq.(1)

Reescrevendo a equação:

$m_a.(v_a_0-v_a)=m_b.(v_b-v_b_0)$ , eq. (2)

Considerando agora que energia cinética também se conserva, podemos escrever:

$K_0 = K \ \rightarrow \ \frac{1}{2}.(m_a.v_a_0^2 +m_b.v_b_0^2)$ $= \frac{1}{2}.(m_a.v_a^2+m_b.v_b^2)$

Reescrevendo a equação:

$m_a.(v_a_0^2 - v_a^2)=m_b.(v_b^2-v_b_0^2) \ \rightarrow \$

$m_a.(v_a_0 - v_a).(v_a_0 +v_a)$ $= m_b.(v_b - v_b_0).(v_b + v_b_0)$ , eq. (3)

Para finalmente obtermos uma expressão que relacione as velocidades iniciais com as finais, dividimos a equação 3 pela 2:

$\frac{eq. (3)}{eq.(2)} \ \rightarrow \ v_a_0+v_a=v_b+v_b_0 \ \rightarrow \$ $v_a_0 - v_b_0 = v_b -v_a$ , eq. (4)

Perceba que a equação (3) nos revela que o valor das velocidades relativas antes e depois da colisão se preservam, o que faz sentido, já que a energia cinética do sistema é constante.

FORMULA DAS VELOCIDADES FINAIS - COLISÕES ELÁSTICAS: DEMONSTRAÇÃO

eq. (1): $m_a.v_a_0+m_b.v_b_0=m_a.v_a+m_b.v_b \$

eq. (4): $v_a_0-v_b_0=v_b-v_a \ \rightarrow \$ $\huge v_b=v_a_0+v_a-v_b_0$

Agora substituimos a equação obtida a partir da 4 na equação 1:

$m_a.v_a_0+m_b.v_b_0=$ $\huge m_a.v_a+m_b.(v_a_0+v_a-v_b_0) \ \rightarrow \$

$(m_a-m_b).v_a_0+2.m_b.v_b_0=$ $(m_a+m_b).v_a \ \rightarrow \$

$v_a = (\frac{m_a-m_b}{m_a_+m_b}).v_a_0+(\frac{2.m_b}{m_a+m_b}).v_b_0$ , eq. (5)

Para encontrarmos a formala da velocidade final para o corpo b; basta substituirmos a eq. (5) na eq. (4).

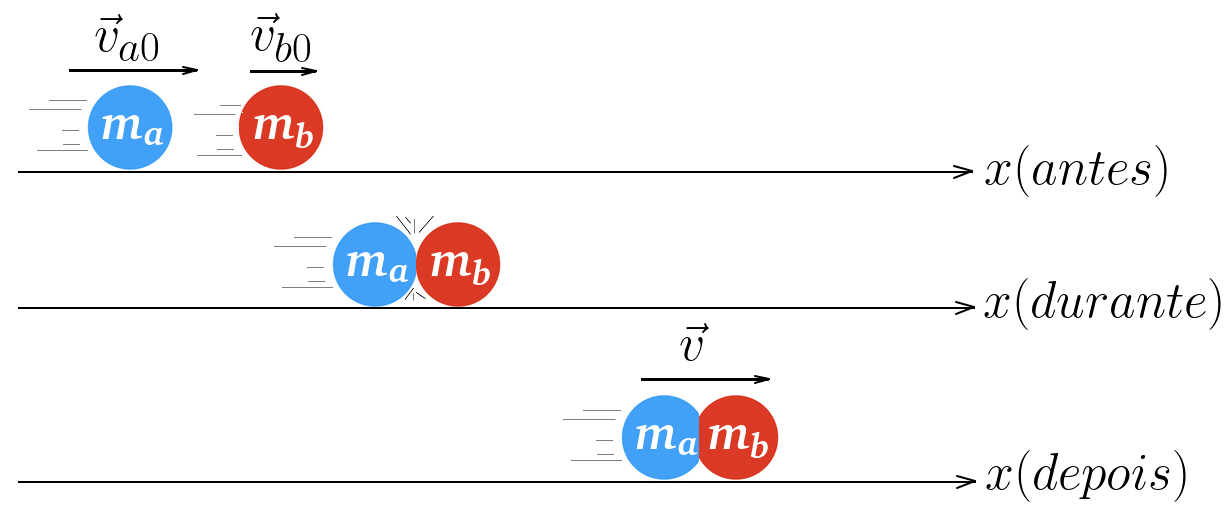
Colisões totalmente inelásticas

Neste tipo de colisão, por um instante, no momento em que os corpos se tocarem, eles aglutinar-se-ão dissipando energia e deste modo, unidos, permacerão a excutar o movimento. Neste tipo de colisão há a maior dissipação possível de energia cinética.