;

Aula

Aula 1.6: Movimento círcular uniforme (MCU)

Chamamos de movimento circular o movimento que se dá sobre uma circunferência ou um arco de circunferência. Iniciaremos os nossos estudos em movimento circular analisando os casos em que este movimento é regido por uma velocidade angular e tangencial constantes. Antes, porém, de falarmos propriamente do movimento, precisamos nos familiarizarmos com o conceito de ângulo e aprender a como manipulá-lo adequadamente para os nossos fins.

Ângulo

O ângulo é medida da inclinação relativa entre dois seguimentos de retas. Ao decorrer de milênios, os humanos convencionaram diferentes modos de se medir esta inclinação, sendo que dois deles se destacaram com singular notoriedade, um deles em virtude de sua simplicidade, o outro, em decorrência de sua utilidade matemática:

Conjunto de pares de retas inclinadas entre si, representando diferentes ângulos


Os sumérios: Há muito tempo, os Sumérios, para se referirem a uma determinada medida angular, convencionaram que quando não há inclinação entre os seguimentos de retas (elas estão, então, paralelas entre si) o valor desta medida seria 0 grau, ao passo que quando a inclinação é máxima, na localização em que, após uma das retas varrer uma circunferência e elas voltarem a ficar paralelas, essa medida valeria 360^° (360 graus) . Após isto, dividiram a circunferência varrida pela reta inclinada em 360 partes iguais, cada qual valeria 1^°. Ainda, cada grau poderia ser divido em 360 partes, cada qual valeria 1' (1 minuto); e os minutos, quando também dividos em 360 partes, dariam origem as frações chamadas segundos. Cada minuto valeria então 1'' (1 segundo). A este sistema descrito chamaremos sistema dos graus.

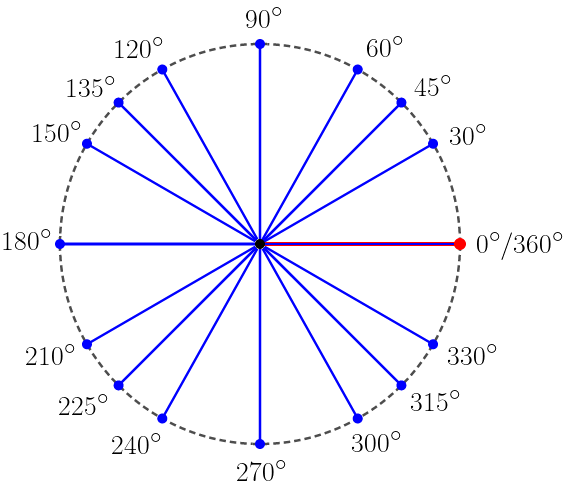
Os sumérios: Há muito tempo, os Sumérios, para se referirem a uma determinada medida angular, convencionaram que quando não há inclinação entre os seguimentos de retas (elas estão, então, paralelas entre si) o valor desta medida seria 0 grau, ao passo que quando a inclinação é máxima, na localização em que, após uma das retas varrer uma circunferência e elas voltarem a ficar paralelas, essa medida valeria 360^° (360 graus) . Após isto, dividiram a circunferência varrida pela reta inclinada em 360 partes iguais, cada qual valeria 1^°. Ainda, cada grau poderia ser divido em 360 partes, cada qual valeria 1' (1 minuto); e os minutos, quando também dividos em 360 partes, dariam origem as frações chamadas segundos. Cada minuto valeria então 1'' (1 segundo). A este sistema descrito chamaremos sistema dos graus.

circulo com marcações em ângulos no sistema de graus

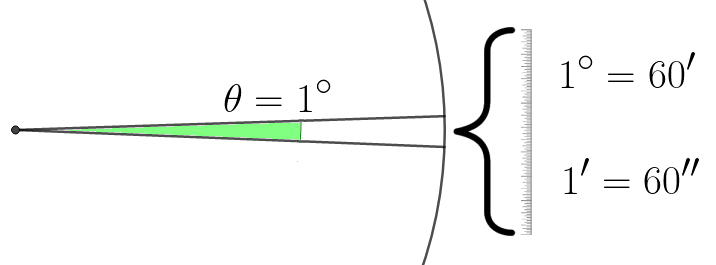
Conversão entre graus, minutos e segundos

Para convertermos graus em minutos ou segundos e vice-versa, basta aplicarmos a relação descrita abaixo em regra de três.

Diagrama para conversão de ângulos de graus para radianos


Os matemáticos da renascença: Mais tarde, afetados pela então criação do cálculo diferencial e integral, os matemáticos, movidos por necessidade inarredável – as quais não convém descrever aqui –, chamaram aquela primeira medida de 0 radiano e a outra de 2π radianos; fazendo nascer assim um novo sistema métrico angular. A este sistema descrito chamaremos sistema dos radianos.

Os matemáticos da renascença: Mais tarde, afetados pela então criação do cálculo diferencial e integral, os matemáticos, movidos por necessidade inarredável – as quais não convém descrever aqui –, chamaram aquela primeira medida de 0 radiano e a outra de 2π radianos; fazendo nascer assim um novo sistema métrico angular. A este sistema descrito chamaremos sistema dos radianos.

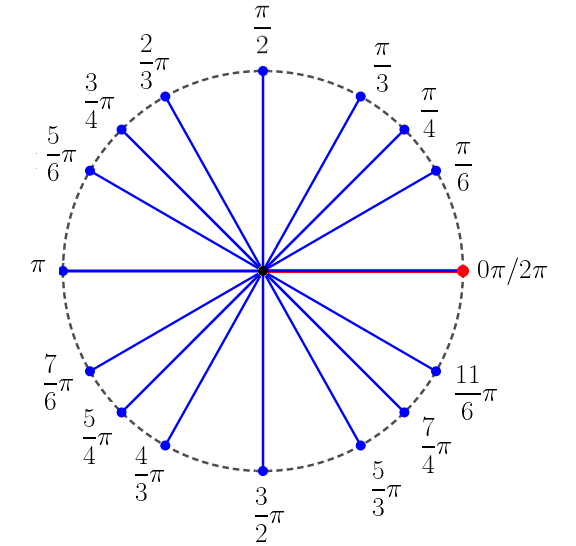
circulo com marcações em ângulos no sistema de radianos

Em física e matemática, hoje, damos prioridade ao sistema de radianos, pois ele é mais versátil do que o anterior. As formulas apresentadas a seguir são prova cabal disto, pois só é valida quando lidamos com ângulos em radianos.


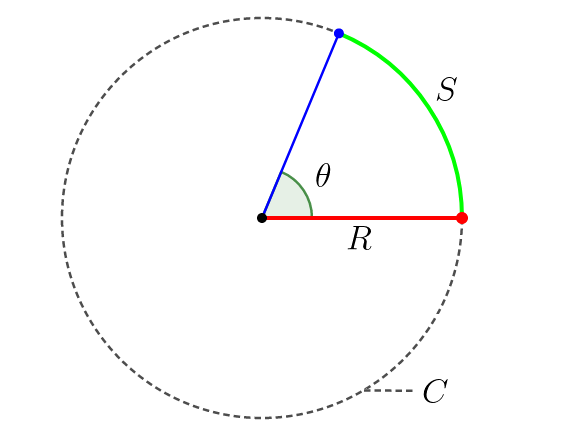
Ângulo em função do arco: O ângulo (θ) é igual a razão do arco de circunferência (S) pelo raio (R) da circunferência: $\theta = \frac{S}{R}$ Circunferência em função do raio: A circunferência (C) é igual ao produto de 2π pelo raio (R): $C = 2.\pi.R$

Ângulo em função do arco: O ângulo (θ) é igual a razão do arco de circunferência (S) pelo raio (R) da circunferência:

$\theta = \frac{S}{R}$

Circunferência em função do raio: A circunferência (C) é igual ao produto de 2π pelo raio (R):

$C = 2.\pi.R$

Circulo com raio, arco de circunferência e ângulo representados

Frequência e perído

Frequência: É a quantidade de ciclos, voltas, eventos etc. por intervalo de tempo.

$f = \frac{n}{\Delta t}$

Veja os exemplos abaixo:

I. A terra rotaciona, ao redor do próprio eixo, 365 vezes por ano (rotações por intervalo de tempo);

II. As lâmpadas piscam 60 vezes por segundo (lampejos por intervalo de tempo);

III. Os alunos têm 5 dias de aula por semana (dias de aulas por intervalo de tempo);

IV. O pêndulo oscila duas vezes por segundo (oscilações por intervalo de tempo);

V. A velocidade do motor é de 1000 RPM (rotações por minuto) (rotações por intervalo de tempo);

Período: é o tempo necessário para que ocorra um ciclo, uma volta, um evento etc.

$T = \frac{\Delta t}{n}$

I. A terra leva 1/365 anos para rotacionar uma vez ao redor do próprio eixo (intervalo de tempo para uma rotação).

II. A cada 1/60 segundos as lâmpadas pistam uma vez (intervalo de tempo para um evento).

III. A cada 7/5 semanas os alunos têm uma aula (intervalo de tempo para um evento).

IV. a cada 1/2 segundo o pêndulo oscila uma vez (intervalo de tempo para uma oscilação).

V. A cada 1/1000 minutos é completado uma rotação no motor (intervalo de tempo para rotação).

Conversão de frequência em período e vice-versa

$T = \frac{1}{f}$ ou $f = \frac{1}{T}$

Velocidade angular média


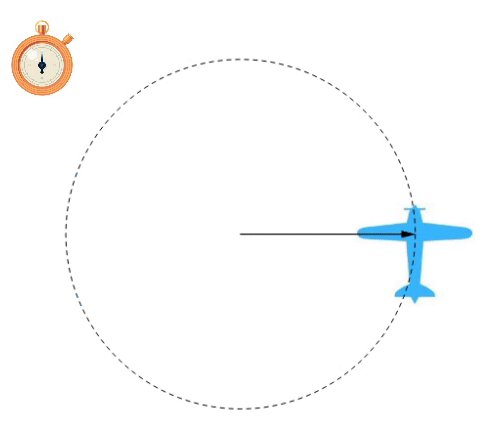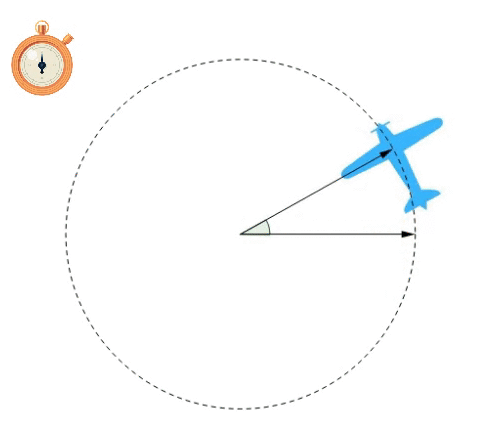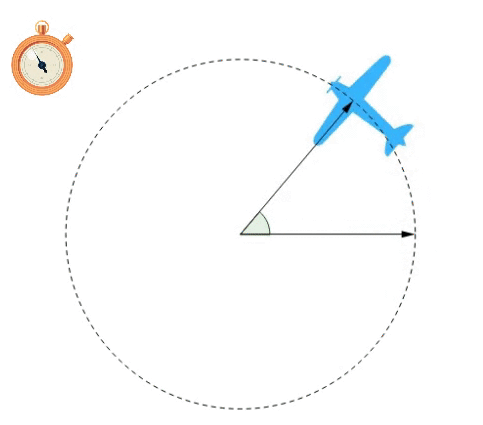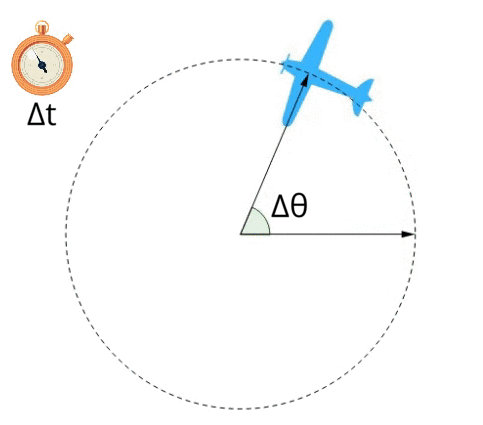
	A velocidade angular média é a grandeza que indica a quantidade de variação do ângulo por intervalo de tempo. Logo, a fórmula que nos fornece ela é: $\omega = \frac{\Delta \theta}{\Delta t}$ ou $w = \frac{2.\pi}{T}$ Teremos como unidade de medida: $[w] = \frac{rad}{s}$ Obs.: No MCU esta grandeza se mantém constante.

A velocidade angular média é a grandeza que indica a quantidade de variação do ângulo por intervalo de tempo. Logo, a fórmula que nos fornece ela é:

$\omega = \frac{\Delta \theta}{\Delta t}$ ou $w = \frac{2.\pi}{T}$

Teremos como unidade de medida:

$[w] = \frac{rad}{s}$

Obs.: No MCU esta grandeza se mantém constante.

Velcidade linear média (velocidade tangencial)


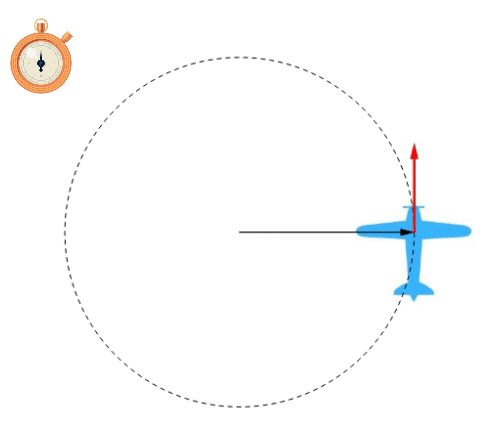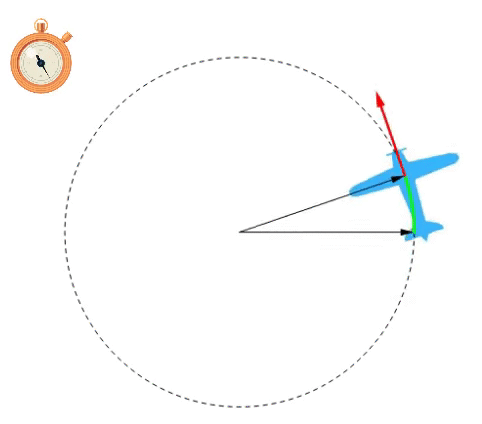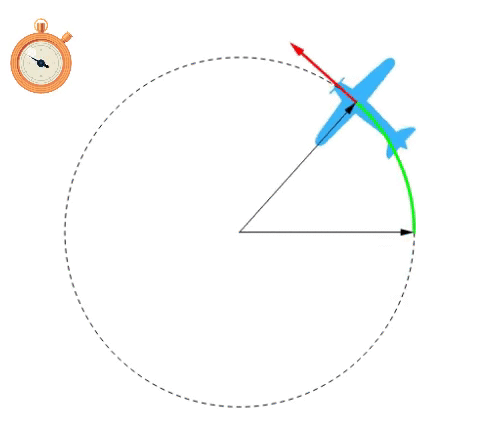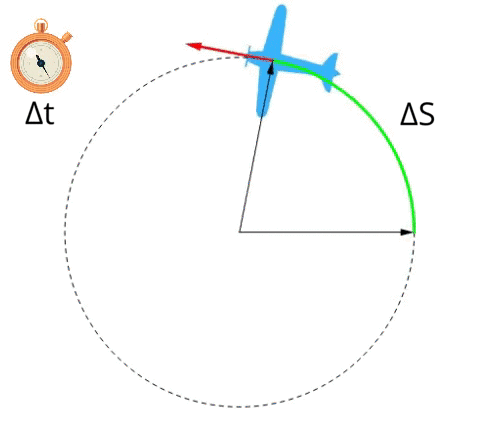
	É a grandeza que indica como a posição, sobre a circunferência percorrida, se altera com o tempo. É uma velocidade que se projeta tangencialmente a trajetória. Na imagem ao lado, está representada pelo vetor vermelho. Para calculá-la, aplicamos a fórmula: $v = \frac{\Delta S}{\Delta t}$ ou $v=\frac{2.\pi.r}{T} = \frac{2.\pi}{T}.r \rightarrow$ $v = \omega.R$

É a grandeza que indica como a posição, sobre a circunferência percorrida, se altera com o tempo. É uma velocidade que se projeta tangencialmente a trajetória. Na imagem ao lado, está representada pelo vetor vermelho. Para calculá-la, aplicamos a fórmula:

$v = \frac{\Delta S}{\Delta t}$ ou $v=\frac{2.\pi.r}{T} = \frac{2.\pi}{T}.r \rightarrow$ $v = \omega.R$

Equação horária do espaço angular

Equação que fornece o ângulo em função do tempo.

Demonstração:

$w=\frac{\Delta \theta}{\Delta t}=\frac{\theta-\theta_0}{t}\rightarrow\theta-\theta_o=w.t$ $\rightarrow \theta=\theta_o+w.t$

Fórmula final:

$\theta = \theta_0 + \omega .t$