Aula

Lista de Exercícios

Aula 7-60: Análise algébrica das lentes esféricas

Equação de Gauss

No estudo de lentes, aplica-se, também, com a mesma convenção de sinais, a equação de gauss (estudada em aulas anteriores):

$\frac{1}{f}=\frac{1}{p}+\frac{1}{p'}$

É importante ressaltar que em se tratando de lentes, o foco será negativo para lentes convergentes e assumirá valor negativo para lentes divergentes

Aumento linear transversal

É um coeficiente que indica o tamanho da imagem gerada (conceito já estudado em aulas anteriores):

$A = \frac{i}{o} = \frac{-p'}{p}$

Equação dos construtores de lentes (equação de Halley)


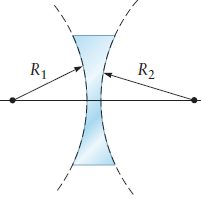
	Como aprendemos anteriormente, as lentes esféricas são formadas a partir da intersecção entre duas esferas. Assim sendo, o foco dependerá dos raios destas esferas, segundo a seguinte expressão: $\frac{1}{f}=(\frac{n_l}{n_m}-1)(\frac{1}{R_1}+\frac{1}{R_2})$ Em que: ◦ f é o foco ◦ n_l é o índice de refração da lente ◦ n_m é o índice de refração do meio ◦ R₁ e R₂ são os raios das esferas que originam as lentes (R será positivo sempre que o círculo formar uma face côncava, se for convexa, ele assumirá um valor negativo)

Como aprendemos anteriormente, as lentes esféricas são formadas a partir da intersecção entre duas esferas. Assim sendo, o foco dependerá dos raios destas esferas, segundo a seguinte expressão:

$\frac{1}{f}=(\frac{n_l}{n_m}-1)(\frac{1}{R_1}+\frac{1}{R_2})$

Em que:

◦ f é o foco

◦ n_l é o índice de refração da lente

◦ n_m é o índice de refração do meio

◦ R₁ e R₂ são os raios das esferas que originam as lentes (R será positivo sempre que o círculo formar uma face côncava, se for convexa, ele assumirá um valor negativo)

Vergência da lente (V)

É um coeficiente que indica a capacidade da lente em convergir ou divergir os raios:

$V = \frac{1}{f}$

A unidade de medida para a vergência é:

$[V] = \frac{1}{m}=di (dioptrias)$