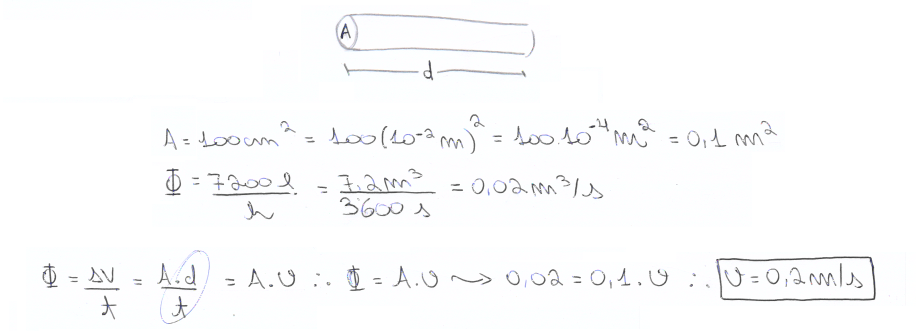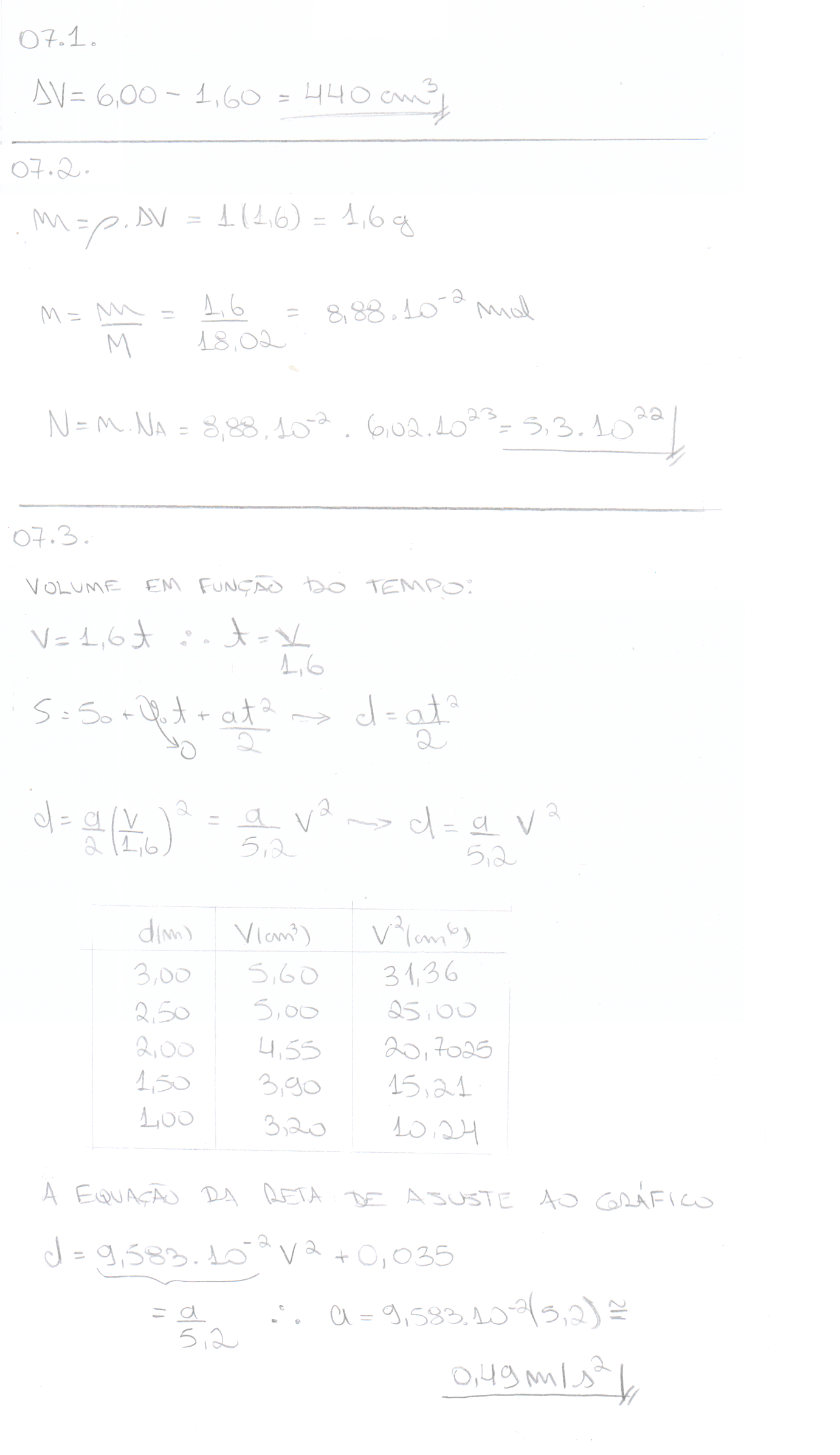Lista 5-37: Hidrodinâmica

01. (ITA-SP) Durante uma tempestade, Maria fecha a janela de seu apartamento e ouve zumbido do vento lá fora.

Subitamente o vidro de uma janela se quebra. Considerando que o vento tenha soprado tangencialmente à janela, o acidente pode ser melhor explicado pelo(a):

02. (Enem 2014) Uma pessoa, lendo o manual de uma ducha que acabou de adquirir para a sua casa, observa o gráfico, que relaciona a vazão na ducha com a pressão, medida em metros de coluna de água (mca).

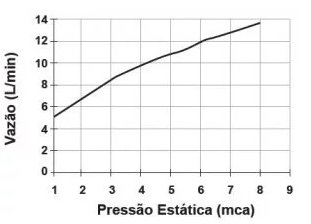
Nessa casa residem quatro pessoas. Cada uma delas toma um banho por dia, com duração média de 8 minutos, permanecendo o registro aberto com vazão máxima durante esse tempo. A ducha é instalada em um ponto seis metros abaixo do nível da lâmina de água, que se mantém constante dentro do reservatório.

Ao final de 30 dias, esses banhos consumirão um volume de água, em litros, igual a

03. (UFSM) Em uma cultura irrigada por um cano que tem área de secção reta de 100 cm², passa água com uma vazão de 7200 litros por hora.

A velocidade de escoamento da água nesse cano, em m/s, é

04. (UFSM) Um fluido ideal percorre um cano cilíndrico em regime permanente. Em um estrangulamento onde o diâmetro do cano fica reduzido à metade, a velocidade do fluido fica:

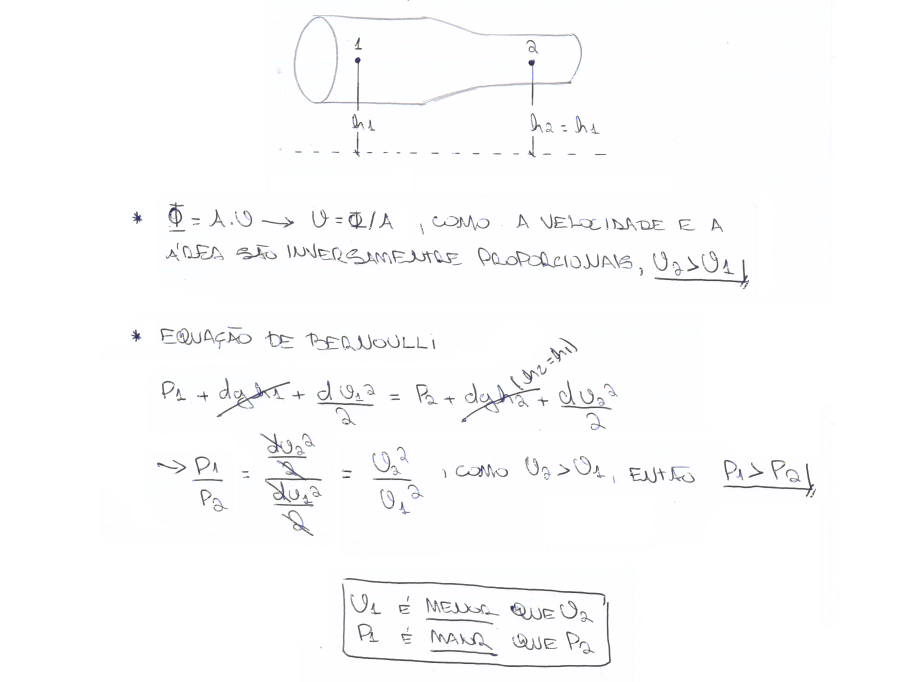
05. (UFSM) A figura representa uma tubulação horizontal em que escoa um fluido ideal.

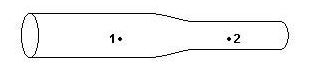
A velocidade de escoamento do fluido no ponto 1, em relação à velocidade verificada no ponto 2, e a pressão no ponto 1, em relação à pressão no ponto 2, são:

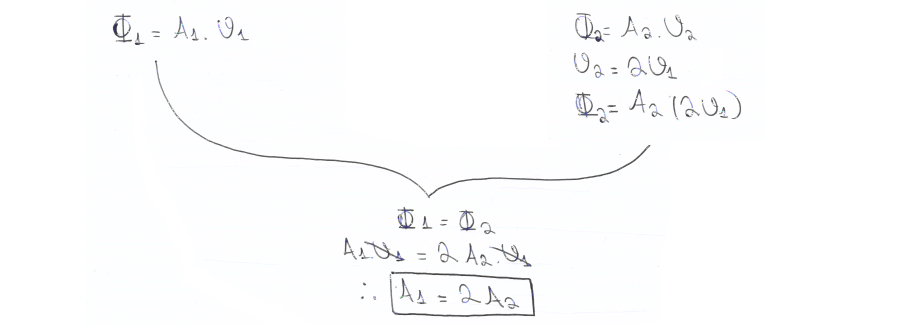
06. (UFRJ) Um jardineiro dispõe de mangueiras de dois tipos, porém com a mesma vazão. Na primeira, a água sai com velocidade de módulo V e, na segunda, sai com velocidade de módulo 2V. A primeira mangueira apresenta:

07. (EXAME NACIONAL 2020) Na recriação da experiência de Galileu, foi utilizado um plano inclinado, de comprimento L , que está esquematizado na Figura 1. Em dois dos ensaios realizados, a esfera foi largada de duas posições diferentes, A e B, tendo-se medido o tempo que a esfera demorou a atingir a posição C.

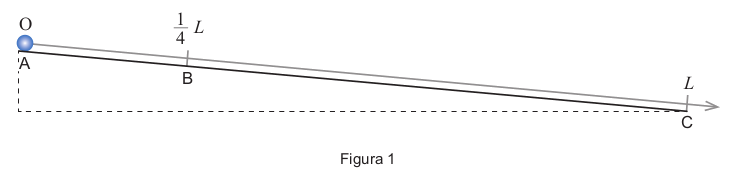
Os tempos de descida da esfera sobre o plano inclinado foram medidos indiretamente a partir dos volumes de água vertidos por uma bureta. Assim, em cada ensaio realizado, abriu-se a torneira da bureta no instante em que a esfera foi largada sobre o plano inclinado e fechou-se a torneira da bureta no instante em que a esfera atingiu a base do plano.

07.1. Na Figura 2, reproduzem-se duas fotografias ( I e II ) de parte da bureta, graduada em cm 3 , nas quais se observa o nível da água no início ( I ) e no final ( II ) de um dos ensaios.

Qual foi o volume de água escoado nesse ensaio?

Apresente o valor solicitado com o número correto de algarismos significativos.

07.2. Considere que, nos ensaios realizados, a bureta vertia, aproximadamente, 1,6 cm³ de água em cada segundo. A massa volúmica da água, nas condições em que foram realizados esses ensaios, é 1,0 g cm^-3 .

Quantas moléculas de água foram, aproximadamente, vertidas pela bureta em cada segundo?

(A) 6,8 x 10²⁴

(B) 9,6 x 10²³

(C) 3,8 x 10²³

(D) 5,3 x 10²²

07.3. Na tabela seguinte, estão registadas as distâncias, d , percorridas pela esfera, largada de diferentes posições sobre o plano inclinado, e os volumes, V , de água vertidos até a esfera atingir a base do plano.

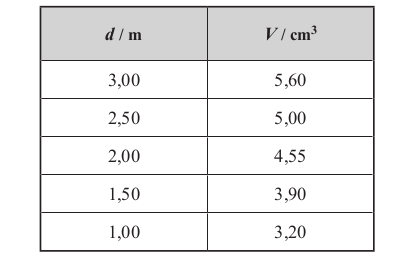
Determine o módulo da aceleração da esfera, em m s - 2 , a partir da equação da reta de ajuste a um gráfico adequado.

Na resposta:

— Apresente uma tabela com os valores a utilizar na construção do gráfico, identificando as variáveis consideradas;

— apresente a equação da reta de ajuste a esse gráfico;

— calcule o valor solicitado.

Explicite o seu raciocínio, indicando todos os cálculos efetuados.