Lista 2-13: Força elástica, lei de Hooke e associação de molas

01. Uma pessoa com massa de 80 kg está sobre uma plataforma cuja base é formada por molas idênticas. Calcule a constante elástica das molas, sabendo que as molas sofreram deformação de 2 cm.

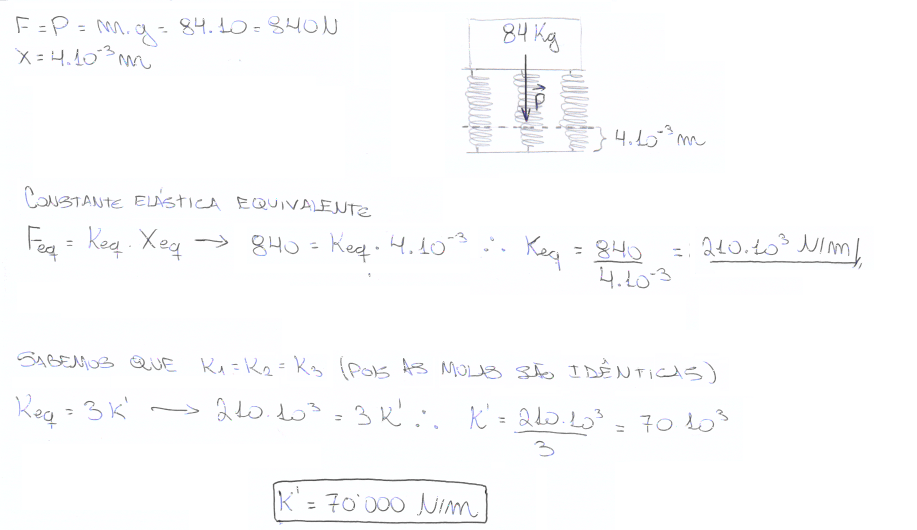
02. Para proteção e conforto, os tênis modernos são equipados com amortecedores constituídos de molas. Um determinado modelo, que possui três molas idênticas, sofre uma deformação de 4 mm ao ser calçado por uma pessoa de 84 kg. Considerando-se que essa pessoa permaneça parada, a constante elástica de uma das molas será, em kN/m, de:

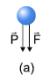
03. Uma bolinha pendurada na extremidade de uma mola vertical executa um movimento oscilatório. Na situação da figura, a mola encontra-se comprimida e a bolinha está subindo com velocidade V. Indicando por F a força da mola e por P a força peso, aplicadas na bolinha, o único esquema que pode representar tais forças na situação descrita é:

04.

Um bloco de peso P está ligado a uma mola ideal de constante elástica K e inicialmente sem deformação, como indica a figura. Quando se solta o bloco, este cai verticalmente esticando a mola. Desprezando-se o efeito do ar, a deformação da mola quando o bloco atinge sua velocidade máxima vale:

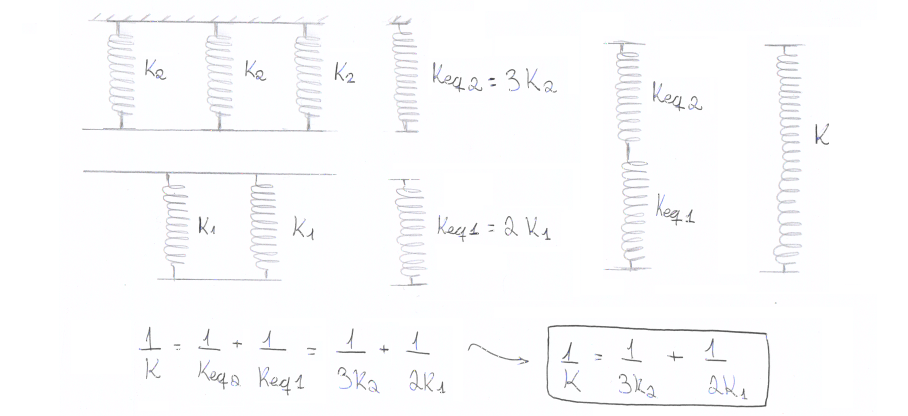
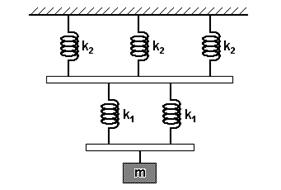
05. Encontre a constante elástica equivalente Keq do sistema em função de K1 e K2:

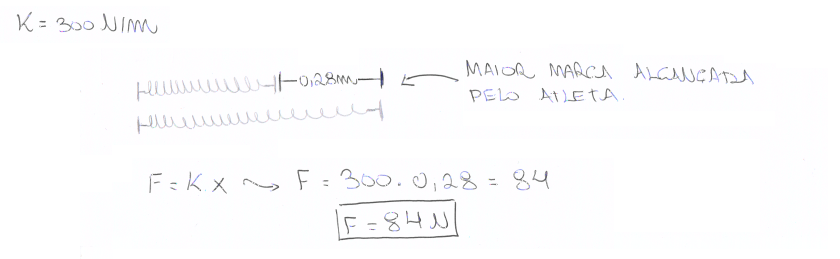
06. (UFSM) Durante os exercícios de força realizados por um corredor, é usada uma tira de borracha presa ao seu abdômen. Nos arranques, o atleta obtém os seguintes resultados:

O máximo de força atingido pelo atleta, sabendo-se que a constante elástica da tira é de 300 N/m e que obedece à lei de Hooke, é, em N:

07. Um vendedor de bolinhas de gude vende seu produto por peso, sendo que 200 g de bolinhas custam R$ 2,00. A balança que o vendedor usa consiste de uma mola de 5 cm com uma das extremidades presas ao teto; a outra extremidade sustenta um recipiente de massa muito pequena onde ele coloca o produto a ser pesado, conforme mostra a figura. O gráfico a seguir indica a calibração do peso do produto em função do comprimento da mola.

Quando são colocadas 5 bolinhas no cesto, observa-se que o comprimento da mola é de 15 cm. Assim, pode-se afirmar que a massa e o custo de cada bolinha são, respectivamente, (considere a aceleração da gravidade sendo 10 m/s²)